Sparsity and the Expectation-Propagation Algorithm

The sparse online GPs of the previous chapter (presented in Section 3.6) can process arbitrarily large datasets. This is possible by avoiding the increase of the GP parameter set using KL-projections to a constrained family of GPs. The drawback of the algorithm stems from its online nature: each example can be processed only once. Indeed, when using the same example in a second iteration there are artifacts caused by treating the already seen data point as independent from the model. This single iteration also means that the solution is dependent on the order of the presentation of the inputs, an unwanted result. If the size of the data is large, then it can be argued that the resulting GP becomes independent of the ordering, but the single processing is disadvantageous if we want to improve the GP when we have smaller datasets and enough computational power for multiple processing.

Recently, an extension to the online learning was proposed by [46], named the expectation-propagation (EP) algorithm. This algorithm improves the result of the Bayes online learning by making possible additional processing of the examples. The algorithm stores the contribution of each example to the approximated posterior. At each online learning step, before processing a data likelihood, the contribution of that specific example is first ``subtracted'' from the approximated posterior. The result is a fixed-point iterative algorithm that repeatedly processes each single data likelihood and converges to a solution that is independent of the order the data is processed. The EP algorithm stops when there are no changes in the individual contributing terms for a full cycle through the data. It has been shown in [46] that the fixed point of the algorithm coincides with the fixed point of the TAP approximation, a statistical physics method that was applied to approximate the posteriors [53], more details in Section 4.2.

The EP algorithm was applied to GPs and it showed improvements over the single-sweep online learning [46]. The EP algorithm in its original form also suffers from the bad scaling of GPs, being of restricted use. In this chapter we combine the EP and the sparse online algorithm for the GPs.

The EP algorithm is discussed in Section 4.1 and then applied to GPs in Section 4.2. The EP algorithm induces an alternative parametrisation to the posterior GP: it is written as the prior and a product of conjugates of the posterior family, the contribution of the individual examples. The connection between the EP-parametrisation and the one based on the parametrisation lemma is presented in Section 4.3. The equivalence of the parametrisations provides the ground for extending the sparse projection method to the EP algorithm (Section 4.4). The algorithm is sketched in Section 4.6 and the chapter finishes with conclusions and discussions.

Expectation-Propagation

Expectation-propagation (EP) [46] is based on the Bayesian online learning presented in Chapter 2 (also in [25]). Since EP exploits and extends the iterations in the online learning, we first sketch online learning and then present the EP algorithm. Let us denote with $\theta$ $\in$ $\mathbb {R}$^m the set of model parameters. We want to infer their distribution q($\theta$). The prior over the parameters is q₀($\theta$) and, as previously, we assume a factorising likelihood:

$$\cal {D} \theta \prod_{k=1}^{N} \tau_{k}^{} \theta$$ (97)

where {(x₁,y₁),...,(x_N,y_N)} is the data set and $\tau_{i}^{}$(y_i,x_i|$\theta$) is the likelihood function. To simplify the notation, in the following the inputs (x_k,y_k) will be suppressed from the likelihood function, being encoded in its index.

We denote by q⁽ⁿ⁾($\theta$) the Bayesian posterior obtained from including all data points up to, and including index n:

$$\theta {\frac{q_0({\boldsymbol { \theta } })\;\prod_{k=1}^n \tau _k({\bo... ...{\boldsymbol { \theta } })\; \prod_{k=1}^n \tau _k({\boldsymbol { \theta } })}}$$ (98)

and observe that we have a recursive relation:

$$\theta {\frac{\tau _n({\boldsymbol { \theta } })q_{post}^{(n-1)}({\bolds... ...\tau _n({\boldsymbol { \theta } })q_{post}^{(n-1)}({\boldsymbol { \theta } })}}$$ (99)

In Chapter 2 different approximation techniques to the intractable posterior have been presented (section 2.2.2) with the focus on online learning: eq. (52) [55]. In Bayesian online learning the approximation to the true posterior q_post^(N)($\theta$) including all examples is obtained by a succession of approximating steps to compute $\hat{q}^{(n)}_{}$($\theta$), an approximation to q_post⁽ⁿ⁾($\theta$).

This is an iterative procedure where we use $\hat{q}^{(n-1)}_{}$($\theta$), the result from the previous online approximation. The posterior is found by applying eq. (99) with $\hat{q}^{(n-1)}_{}$($\theta$) instead of q^{(n - 1)}($\theta$). Since q⁽ⁿ⁾_post is also intractable, a second approximation step is used to obtain $\hat{q}^{(n)}_{}$. This is formally written as

$$\hat{q}_{n}^{} \theta \longleftarrow {\frac{\tau _n({\boldsymbol { \theta } })\hat{q}_{n-1}({\boldsymb... ...\; \tau _n({\boldsymbol { \theta } })\hat{q}_{n-1}({\boldsymbol { \theta } })}}$$ (100)

where the arrow specifies a projection of the intractable posterior to a tractable family of distributions. Performing the iterations for all data gives $\hat{q}_{N}^{}$ which depends on the order of presentation. Unless new data arrives it is impossible to improve on the online result.

The goal of expectation propagation is to apply further iterations of the updates for the posterior distribution, thus producing a better approximation than the result from online algorithm alone. To achieve this, we ``unfold'' $\hat{q}^{(N)}_{}$, the end-result of the online iterations, as

$$\hat{q}_{N}^{} \theta \theta \prod_{n=1}^{N} {\frac{\hat{q}_n({\boldsymbol { \theta } })}{\hat{q}_{n-1}({\boldsymbol { \theta } })}}$$ (101)

The observation made by [46] is that each factor in the product corresponds to an approximation of the corresponding likelihood term, since that has been the basis of the update for $\hat{q}^{(n)}_{}$ from eq. (100). In the following $\hat{\tau }_{n}^{}$($\theta$) = $\hat{q}_{n}^{}$($\theta$)/$\hat{q}_{n-1}^{}$($\theta$) will be used and we will call this ratio as approximating likelihood.

Using these notations, the Bayesian update is rewritten as a problem of estimating the individual factors $\hat{\tau }_{n}^{}$($\theta$) which give the approximate posterior distribution:

$$\hat{q}_{N}^{} \theta \theta \prod_{n=1}^{N} \hat{\tau }_{n}^{} \theta$$ (102)

The above relation is usable only if the prior distribution and the approximated posterior belong to the family of the exponential distributions [3]. Then, since it is the ratio of two exponentials, the approximating likelihood is also in the exponential family: $\hat{\tau }_{i}^{}$($\theta$) is conjugate to the prior. The approximating likelihoods used with the prior distribution lead to a tractable posterior, without the need for any approximation. Further we see the possible benefits of using the approximating likelihoods: the approximations to $\tau_{i}^{}$($\theta$) are made locally, weighted by $\hat{q}^{(n-1)}_{}$($\theta$).

To improve on each term $\hat{\tau }_{k}^{}$($\theta$) using online learning, we first have to find the distribution $\hat{q}^{(k-1)}_{}$ = $\hat{q}^{\setminus k}_{}$($\theta$) independent of the likelihood $\tau_{k}^{}$($\theta$). This is done by removing $\hat{\tau }_{k}^{}$($\theta$) from the posterior eq. (102). This implies that we have to keep the approximated likelihoods for all data. The online learning used here was presented in Chapter 2. It minimises a KL-distance [14] by matching the moments of the true and the approximated posterior (see Section 2.2.2).

If an input $\tau_{k}^{}$($\theta$) has already been seen, we need to remove its contribution $\hat{\tau }_{k}^{}$($\theta$) from the current parameter estimate before using the online step from Section 2.4. This is done by ``subtracting'' it from the posterior and the online learning rule is performed with the adjusted prior:

$$\hat{q}^{\setminus k}_{} \theta {\frac{q_0({\boldsymbol { \theta } })\;\prod^{\setminus k}_n\hat{... ...{ \theta } })\; \prod^{\setminus k}_n\hat{\tau }_n({\boldsymbol { \theta } })}}$$ (103)

where the second term on the right does not depend on $\theta$, the parameter being integrated out. Using the modified prior $\hat{q}^{\setminus k}_{k}$ and the likelihood-term $\tau_{k}^{}$($\theta$), the posterior $\hat{q}_{k}^{}$($\theta$) is:

$$\hat{q}^{new}_{k} \theta \longleftarrow {\frac{u_{k}({\boldsymbol { \theta } })\;\hat{q}({\boldsymbol { \... ...ta } }\; u_{k}({\boldsymbol { \theta } })\;\hat{q}({\boldsymbol { \theta } })}} \theta {\frac{{\tau }_{k}({\boldsymbol { \theta } })}{\hat{\tau }_{k}({\boldsymbol { \theta } })}}$$ (104)

Since $\hat{\tau }_{i}^{}$($\theta$) appears both in the numerator and the denominator, its normalising constants are irrelevant. This means that in the numerical implementation of the algorithm it will be enough to store the terms of the exponentials of $\theta$. On the other hand, an exact computation of each normalising constant would be required if we want to approximate the evidence of the model, considered by [46]. In this thesis the model selection issue is not addressed, however, it is a very important area of future research. The new $\hat{\tau }_{k}^{}$ is computed as

$$\hat{\tau }^{new}_{k} \theta {\frac{\hat{q}^{new}_{k}({\boldsymbol { \theta } })}{\hat{q}^{\setminus k}_k}} \propto {\frac{\hat{q}^{new}_{k}({\boldsymbol { \theta } })}{\hat{q}_k({\boldsymbol { \theta } })}} \hat{\tau }_{k}^{} \theta$$ (105)

In the EP iterations we choose - randomly or by using different heuristics - an index k and apply online learning for that example. The cycle terminates if there are no changes in the approximated likelihoods $\hat{t}_{i}^{}$($\theta$). We do not have a guaranteed global convergence but the system usually finds a fixed point and this minimum point is independent of the order of inclusion of the individual likelihoods.

Figure 4.1: Visualisation of the expectation propagation algorithm. The likelihoods are ``projected'' to the parametric family $\cal {P}$, they can be interpreted as one-dimensional vectors. The final approximation is the result of combining the prior with the projection terms: graphically this is done by adding the line segments $\hat{\tau }_{i}^{}$ to the prior process p₀.

The visualisation of the EP algorithm with the approximate likelihoods $\hat{\tau }_{i}^{}$($\theta$) is shown in Fig. 4.1. Whilst in the usual online learning at the end of the N-th iterations $\hat{q}_{N}^{}$($\theta$) is the approximated posterior, in this case the online steps are used to improve on the approximation of the individual ``segments'' $\hat{\tau }_{n}^{}$ that build up $\hat{q}_{N}^{}$($\theta$). The similarity of Fig. 4.1 with online learning as presented in Fig. 2.2 illustrates that the EP algorithm is built on the online method. The underlying dynamics is different in the two cases: for online learning we have only the ``path'' toward the final approximation. In contrast, for the EP algorithm the emphasis is on building up the chain that links the prior with the posterior. If we take logarithms in eq. (102), then $\hat{\tau }_{i}^{}$ is the difference between two log-probabilities. Further, if we consider $\hat{q}_{t+1}^{}$ and $\hat{q}_{t}^{}$ as points in the space of distributions, then $\hat{\tau }_{i}^{}$ is a one-dimensional line connecting the two distributions, as shown in Fig. 4.1. A first online sweep is used to initialise the individual terms $\hat{\tau }_{k}^{}$. Alternatively the terms can be initialised with a constant value 1, having p₀ = $\hat{p}_{N}^{}$ in the beginning.

To sum up, the EP extension of the online learning algorithm from Chapter 2 implies:

• iterations over the individual data points until convergence,
• the storage of the projected individual likelihood terms $\hat{t}_{k}^{}$ for each data, and
• ``subtracting'' the approximated likelihood $\hat{\tau }_{k}^{}$($\theta$) from the posterior before applying the online learning.
• terminating when the equilibrium is reached, that is when none of the approximated likelihoods changes.

The benefit of the EP algorithm is that it allows data processing beyond online learning, the extra cost, apart from the increased computational time, is the additional storage of the projected likelihood terms. The EP algorithm will be applied to GPs in the next section.

EP for Gaussian Processes

In the following the feature-space notation and the GP parametrisation from the parametrisation lemma 2.3.1 is used. Similarly to the intuition behind deducing the KL-divergences, the feature space formalism provides us with a more intuitive picture of the algorithm. The EP algorithm applied to GP classification was presented in [46, Chapter 5]. In this chapter we will leave the likelihood unspecified, the EP procedure being identical for other likelihoods also.

We assume that we are given the kernel K₀(x,x^$\prime$) and we consider the feature space $\pmb$$\cal {F}$and the scalar product generated by the kernel: if $\phi_{\boldsymbol { x } }^{}$ is the projection of the x into the unknown $\cal {F}$, then we have K₀(x,x^$\prime$) = $\phi^{T}_{\boldsymbol { x } }$$\phi_{{\boldsymbol { x } }'}^{}$ [95,93]. Using the feature space, the GP is equivalent to normal distribution for the parameter vector f in $\pmb$$\cal {F}$: ${\boldsymbol { f } }\sim{\ensuremath{{\mathcal{N}}}}({\boldsymbol { \mu } },\ensuremath{{\boldsymbol { \Sigma } }})$, as shown in Chapter. 2, eq. (48). ${\ensuremath{{\mathcal{N}}}}({\boldsymbol { \mu } },\ensuremath{{\boldsymbol { \Sigma } }})$ is a normal distribution with mean and covariance given by:

$$\begin{split}{\boldsymbol { \mu } }&= {\boldsymbol { \mu } }_... ...hi } }{\boldsymbol { C } }{\boldsymbol { \Phi } }^T \end{split}$$ (106)

with $\alpha$ = [$\alpha_{1}^{}$,...,$\alpha_{N}^{}$]^T, C = {C_ij}_{i, j = 1, N} the parameters of the GP and $\Phi$ = [$\phi_{1}^{}$,...,$\Phi_{N}^{}$]^T is the concatenation of all feature vectors from the $\cal {BV}$ set and ${\boldsymbol { I } }_{\ensuremath{\pmb{\cal{F}}}}$ is the identity matrix in the feature space. In the following we assume $\mu$ = 0. At this point we also assume that the learning rules do not include sparsity and the set of basis vectors coincides with the input data, the sparse case being discussed later in Section 4.4.

We use the ``time'' index t, and assume that $\tau_{t+1}^{}$(f) is a likelihood chosen from the data set. The online updates, assuming that $\tau_{t+1}^{}$(f) was not previously processed, are (eq. 54):

$$\begin{split}{\boldsymbol { \mu } }_{t+1} &= {\boldsymbol { \... ...phi_{t+1}^T\ensuremath{{\boldsymbol { \Sigma } }}_t \end{split}$$ (107)

with $\phi_{t+1}^{}$ $\doteq$ $\phi_{{\boldsymbol { x } }_{t+1}}^{}$ and the scalars q^{(t + 1)} and r^{(t + 1)} given in eq. (53). We have to find the approximate likelihood $\hat{t}_{t+1}^{}$(f), the ratio of the approximated posterior GPs at time t + 1 and t respectively. From the definition of $\hat{t}_{t+1}^{}$ in eq. (102) we have:

$$\begin{split}\hat{t}_{t+1} &= \frac{{\ensuremath{{\mathcal{N}... ... { \mu } }_t-{\boldsymbol { f } }) \right] \right\} \end{split}$$ (108)

To simplify the expression for $\hat{t}_{t+1}^{}$, we first express the update rule for the inverse covariances in the feature space using the matrix inversion lemma (eq. (181) and [43]):

$$\begin{split}\ensuremath{{\boldsymbol { \Sigma } }}_{t+1}^{-1... ...} &= \frac{-r^{(t+1)}}{1 + r^{(t+1)}\sigma^2_{t+1}} \end{split}$$ (109)

where $\sigma_{t+1}^{2}$ = $\phi^{T}_{t+1}$$\Sigma$$\phi_{t+1}^{}$ = k^* + k_{t + 1}^TCk_{t + 1} is the predictive variance of the GP at time t and at location x_{t + 1}. We define

$$\begin{split}u_{t+1} &\doteq \phi_{t+1}^T{\boldsymbol { f } }... ..._{t+1} &\doteq \phi_{t+1}^T{\boldsymbol { \mu } }_t \end{split}$$ (110)

the projection of the random variable f and the mean where the projection vector is $\phi_{t+1}^{}$. The exponential term in (108) is rewritten as

$${\frac{\lambda_{t+1}}{2}} \left(\vphantom{u_{t+1} -m_{t+1} + \frac{q^{(t+1)}}{r^{(t+1)}}}\right. {\frac{q^{(t+1)}}{r^{(t+1)}}} \left.\vphantom{u_{t+1} -m_{t+1} + \frac{q^{(t+1)}}{r^{(t+1)}}}\right)^{2}_{} {\frac{r^{(t+1)}}{2}} \left(\vphantom{\frac{q^{(t+1)}}{r^{(t+1)}}}\right. {\frac{q^{(t+1)}}{r^{(t+1)}}} \left.\vphantom{\frac{q^{(t+1)}}{r^{(t+1)}}}\right)^{2}_{}$$ (111)

and the ratio of the determinants becomes

$$\left\vert\vphantom{\frac{\ensuremath{{\boldsymbol { \Sigma } }}_{t+1}}{\ensuremath{{\boldsymbol { \Sigma } }}_{t}}}\right. {\frac{\ensuremath{{\boldsymbol { \Sigma } }}_{t+1}}{\ensuremath{{\boldsymbol { \Sigma } }}_{t}}} \left.\vphantom{\frac{\ensuremath{{\boldsymbol { \Sigma } }}_{t+1}}{\ensuremath{{\boldsymbol { \Sigma } }}_{t}}}\right\vert^{-1/2}_{} \left(\vphantom{1 + r^{(t+1)}\sigma^2_{t+1}}\right. \sigma^{2}_{t+1} \left.\vphantom{1 + r^{(t+1)}\sigma^2_{t+1}}\right)^{-\frac{1}{2}}_{}$$ (112)

leading to a scalar quadratic expression for the approximated likelihood

$$\hat{t}_{t+1}^{} \left(\vphantom{1 + r^{(t+1)}\sigma^2_{t+1}}\right. \sigma^{2}_{t+1} \left.\vphantom{1 + r^{(t+1)}\sigma^2_{t+1}}\right)^{-\frac{1}{2}}_{} \left[\vphantom{-\frac{\lambda_{t+1}}{2} \left(u_{t+1} - a_{t+1}\right)^2 }\right. {\frac{\lambda_{t+1}}{2}} \left(\vphantom{u_{t+1} - a_{t+1}}\right. \left.\vphantom{u_{t+1} - a_{t+1}}\right)^{2}_{} \left.\vphantom{-\frac{\lambda_{t+1}}{2} \left(u_{t+1} - a_{t+1}\right)^2 }\right]$$ (113)

The parameters a_{t + 1} and $\lambda_{t+1}^{}$ depend on the likelihood and the prior GP:

$$\begin{split}a_{t+1} &= m_{t+1} - \frac{q^{(t+1)}}{r^{(t+1)}}... ...eft( (r^{(t+1)})^{-1} + \sigma_{t+1}^2 \right)^{-1} \end{split}$$ (114)

For a single likelihood this approximation is a one-dimensional Gaussian in the random variable u_{t + 1}. Since model selection is not treated here, we do not have to store the normalising constants for the posterior either. We have to keep only the parameters of the distribution of u_{t + 1}, that is the pair ($\lambda_{t+1}^{}$, a_{t + 1}). The cost is small, requiring 2N scalars. Using again Fig. 4.1 we identify the segment from any $\hat{p}_{k}^{}$ to $\hat{p}_{k+1}^{}$ as pointing to the direction of $\phi_{k+1}^{}$ and parametrised using ($\lambda_{t+1}^{}$, a_{t + 1}).

The prior GP and the approximated likelihood identify the approximated posterior GP; this involves another data-dependent parametrisation. In the following we assume that both the GP parameters ($\alpha$,C) and the scalars (a_i,$\lambda_{i}^{}$) are updated, the relation between the two parametrisations is discussed in Section 4.3.

To perform the online update eqs. (107), first we need to subtract the contribution of the current likelihood from the model. We assume that an example (x_i,y_i) has been picked for processing and the approximated likelihood has the parameters (a_i,$\lambda_{i}^{}$). We compute the new GP with ($\tilde{{\boldsymbol { \mu } }}$,$\tilde{{\boldsymbol { C } }}$) given by the parametrisation lemma 2.3.1:

$${\frac{{\ensuremath{{\mathcal{N}}}}({\boldsymbol { f } }\vert{\bo... ...mbol { \Sigma } }})}{\hat{t}_i(\phi^T{\boldsymbol { f } }\vert a_i,\lambda_i)}} \propto \mathcal {N} \tilde{{\boldsymbol { \mu } }} \tilde{\ensuremath{{\boldsymbol { \Sigma } }}}$$

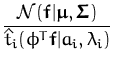Matching the linear and quadratic terms in f leads to

$$\begin{split}\tilde{{\boldsymbol { \mu } }} &= {\boldsymbol {... ...- v_i{\boldsymbol { h } }_i{\boldsymbol { h } }_i^T \end{split} \begin{split}{\boldsymbol { h } }_i &= \ensuremath{{\boldsymb... ...th{{\boldsymbol { \Sigma } }}\phi_i -\lambda_i^{-1} \end{split}$$ (115)

giving us the parameters of the Gaussian with which we can perform the online updates. The next step is to find the changed parameters ($\tilde{{\boldsymbol { \alpha } }}$,$\tilde{{\boldsymbol { C } }}$) of the new GP according to the parametrisation lemma 2.3.1. By substituting the general parametrisation from eq. (106) into eq. (115) we find:

$$\begin{split}\tilde{{\boldsymbol { \alpha } }} &= {\boldsymbo... ...- v_i{\boldsymbol { h } }_i{\boldsymbol { h } }_i^T \end{split} \begin{split}{\boldsymbol { h } }_i &= {\boldsymbol { C } }{\... ...{ e } }_i \\ v_i^{-1} &= \sigma_i^2 -\lambda_i^{-1} \end{split}$$ (116)

where k_i = [K₀(x₁,x_i),..., K₀(x_N,x_i)]^T and $\sigma_{i}^{2}$ = K₀(x_i,x_i) + k_i^TCk_i is the variance of the marginalisation of the GP at x_i.

The EP algorithm for the Gaussian processes can now be established. We select the prior kernel and set $\alpha$ = 0 and C = 0. Similarly, the additional parameters a_i and $\lambda_{i}^{}$ that parametrise the likelihood approximations at the data points are also set to zero. We mention that the zero value for $\lambda_{i}^{}$ simply means v_i = 0 in eqs. (115) and (116).

After selecting an example (x_{t + 1},y_{t + 1}), the approximated likelihood is subtracted from the GP, using eq (116). Then we compute the scalar update coefficients q^{(t + 1)} and r^{(t + 1)} using the ``corrected'' GP and the likelihood t(x_{t + 1}|f) applying the standard online learning procedure, eq. (53). Simultaneously to the online update for the GP parameters ($\alpha$,C) from eq. (57), we also update the coefficients of the projected likelihoods $\hat{t}$(x_{t + 1}) using eqs. (114). The algorithm then processes a subsequent example and stops if none of the parameters (a_i,$\lambda_{i}^{}$) are changed.

The EP algorithm encodes the approximated posterior in the one-dimensional normal distributions and we have to store the mean and the variance. In the statistical physics framework, mean field theory is an approximation technique that uses a simpler parametric form for the posterior distributions to obtain a tractable approximation. Recently mean field methods have been gaining popularity in the machine learning community; the techniques developed originally for statistical physics are applied to machine learning problems in [56]. The ADATAP approach [53] aims at finding the approximate posteriors for models using factorising likelihoods and prior distributions with quadratic terms, as is eq. (98) using Gaussian for p₀(f). The random variables u_i are termed cavity fields and a batch approximation for its distribution is provided using advanced statistical physics methods. The ADATAP method is not discussed here, we only mention that the fixed-point solution of the EP algorithm is the same as this approximation.

The EP learning, as presented in this section, applies to GPs that are fully parametrised, i.e.. they include all data points in their representation. To apply the EP for the sparse GP algorithm, we need the updates for (a_i,$\lambda_{i}^{}$) if an element from the $\cal {BV}$ set is removed. Before deriving the sparse EP algorithm, the relation between the two representations for the same GP is established. The sparse extension will follow from the relations between these two parametrisations. The sparse extension of the EP algorithm will follow from this equivalence, presented in Section 4.4

Relation between GP parametrisations

The posterior GP in the EP-framework is proportional to the prior GP and the product of approximating likelihoods, providing an alternative parametrisation to the GP. The EP representation in this case is via N one-dimensional quadratic exponentials, the approximated likelihood terms. The approximated likelihoods are defined in terms of scalar random variables u_i = $\phi_{i}^{T}$f which are projections of f, the random variable in $\pmb$$\cal {F}$. The resulting GP is written as:

$$\begin{split}{\ensuremath{{\cal{GP}}}}_{post}({\boldsymbol { ... ...ymbol { f } }-{\boldsymbol { a } }) \right]\right\} \end{split}$$ (117)

where $\Lambda$ is a diagonal matrix having $\lambda_{i}^{}$ on the diagonals and a is the vector of the means. The feature vectors are grouped into $\Phi$ = [$\phi_{1}^{}$,...,$\phi_{N}^{}$]^T. We will call this the ``EP-parametrisation''.

The second parametrisation of the same GP is given by the parametrisation lemma and uses ($\alpha$,C) as parameters of the mean and the covariance as shown in eq. (106):

$$\cal {GP} \alpha \propto \left\{\vphantom{-\frac{1}{2}\left({\boldsymbol { f } }- {\boldsy... ...ymbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }\right) }\right. {\textstyle\frac{1}{2}} \left(\vphantom{{\boldsymbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }}\right. \Phi \alpha \left.\vphantom{{\boldsymbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }}\right)^{T}_{} \left(\vphantom{{\boldsymbol { I } }_{\ensuremath{\pmb{\cal{F}}}}+ {\boldsymbol { \Phi } }{\boldsymbol { C } }{\boldsymbol { \Phi } }^T }\right. \pmb \cal {F} \Phi \Phi \left.\vphantom{{\boldsymbol { I } }_{\ensuremath{\pmb{\cal{F}}}}... ...symbol { \Phi } }{\boldsymbol { C } }{\boldsymbol { \Phi } }^T }\right)^{-1}_{} \left(\vphantom{{\boldsymbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }}\right. \Phi \alpha \left.\vphantom{{\boldsymbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }}\right) \left.\vphantom{-\frac{1}{2}\left({\boldsymbol { f } }- {\boldsym... ...mbol { f } }- {\boldsymbol { \Phi } }{\boldsymbol { \alpha } }\right) }\right\}$$ (118)

we term the ``natural parametrisation''. Since we have the same GP in both cases, we can identify the coefficients of f and ff^T in eqs. (117) and (118):

$$\Sigma \mu \pmb \cal {F} \Phi \Phi \Phi \alpha = {\boldsymbol { \Phi } }{\boldsymbol { \Lambda } }{\boldsymbol { a } }$$ (119)

$${\boldsymbol { \Sigma } }^{-1} = ({\boldsymbol { I } }_{\ensuremath{\pmb{\cal{F}}}}+ {\boldsymbol { \Phi } }{\boldsymbol { C } }{\boldsymbol { \Phi } }^T)^{-1} = {\boldsymbol { I } }_{\ensuremath{\pmb{\cal{F}}}}+ {\boldsymbol { \Phi } }{\boldsymbol { \Lambda } }{\boldsymbol { \Phi } }^T .$$ (120)

The matrix inversion lemma will transform the identities into a form where we can identify the components. From the EP-parameters (a,$\Lambda$) we obtain the GP-ones ($\alpha$,C) by

$$\begin{split}{\boldsymbol { \alpha } }&= \left( {\boldsymbol ... ...mbda } }^{-1} + {\boldsymbol { K } }_N \right)^{-1} \end{split}$$ (121)

where K_N is the kernel matrix with respect to all data. Notice that the diagonal form of $\Lambda$ results from the factorising likelihood. The corresponding inverse relation is:

$$\begin{split}{\boldsymbol { a } }&= - {\boldsymbol { C } }^{-... ...bol { C } }^{-1} + {\boldsymbol { K } }\right)^{-1} \end{split}$$ (122)

Inspecting the above equations we see that the matrix C is fully specified by a diagonal matrix of the same size. This implies that we can represent it by the diagonals of $\Lambda$ and use eq. (119) whenever C is needed. Apart from the computational cost of this operation, in case of sparse updates this simplification does not hold any more: $\Lambda$ is not diagonal after removing some of the basis vectors, as will be shown in the next section.

Sparsity and Expectation Propagation

Sparsity is defined using the ``natural parametrisation'' of Chapter 2 with the parameters ($\alpha$,C). The sparse solution is obtained by eliminating some data points from the representation while retaining as much information about the data itself as possible. Using again the equivalence of GPs with Gaussians in the feature space, we want the mean and covariance from eq. (117) to be expressed, instead of the full data vector $\Phi$ = [$\phi_{1}^{}$,...,$\phi_{N}^{}$]^T, by using only a subset of it. We follow the deduction of sparsity from Chapter 3: the last element is removed from the $\cal {BV}$ set, leaving $\hat{{\boldsymbol { \Phi } }}$ = $\Phi$ $\setminus$ {$\phi_{N}^{}$}. The derivation for the case of eliminating more then a single element is very similar.

We assume that we have the EP-parameters (a,$\Lambda$) with respect to the full input data $\Phi$ and we want to obtain the KL-optimal parameters ($\hat{{\boldsymbol { a } }}$,$\hat{{\boldsymbol { \Lambda } }}$) using the restricted set $\hat{{\boldsymbol { \Phi } }}$ of input features. We want to represent the resulting GP using the EP-representation:

$$\hat{{\ensuremath{{\cal{GP}}}}} \hat{{\boldsymbol { a } }} \hat{{\boldsymbol { \Lambda } }} \propto \left\{\vphantom{-\frac{1}{2}\left[{\boldsymbol { f } }^T{\boldsy... ...l { \Phi } }}^T{\boldsymbol { f } }-\hat{{\boldsymbol { a } }}) \right]}\right. {\textstyle\frac{1}{2}} \left[\vphantom{{\boldsymbol { f } }^T{\boldsymbol { f } }+ (\hat... ...ldsymbol { \Phi } }}^T{\boldsymbol { f } }-\hat{{\boldsymbol { a } }}) }\right. \hat{{\boldsymbol { \Phi } }}^{T}_{} \hat{{\boldsymbol { a } }} \hat{{\boldsymbol { \Lambda } }} \hat{{\boldsymbol { \Phi } }}^{T}_{} \hat{{\boldsymbol { a } }} \left.\vphantom{{\boldsymbol { f } }^T{\boldsymbol { f } }+ (\hat... ...ldsymbol { \Phi } }}^T{\boldsymbol { f } }-\hat{{\boldsymbol { a } }}) }\right] \left.\vphantom{-\frac{1}{2}\left[{\boldsymbol { f } }^T{\boldsym... ... { \Phi } }}^T{\boldsymbol { f } }-\hat{{\boldsymbol { a } }}) \right]}\right\}$$ (123)

We start with deducing $\hat{{\boldsymbol { \Lambda } }}$. For this we use the relation between the EP-parameters and the natural parameters for the covariance of the reduced system from eq. (122):

$$\hat{{\boldsymbol { \Lambda } }} \left(\vphantom{\hat{{\boldsymbol { C } }}^{-1}+\hat{{\boldsymbol { K } }}}\right. \hat{{\boldsymbol { C } }}^{-1}_{} \hat{{\boldsymbol { K } }} \left.\vphantom{\hat{{\boldsymbol { C } }}^{-1}+\hat{{\boldsymbol { K } }}}\right)^{-1}_{} \hat{{\boldsymbol { K } }}^{-1}_{} \hat{{\boldsymbol { K } }}^{-1}_{} \left(\vphantom{\hat{{\boldsymbol { C } }}+\hat{{\boldsymbol { K } }}^{-1}}\right. \hat{{\boldsymbol { C } }} \hat{{\boldsymbol { K } }}^{-1}_{} \left.\vphantom{\hat{{\boldsymbol { C } }}+\hat{{\boldsymbol { K } }}^{-1}}\right)^{-1}_{} \hat{{\boldsymbol { K } }}^{-1}_{}$$ (124)

where we used the matrix inversion lemma eq. (181). We can now use the KL-optimal reduction of the matrix C from eq. (79)

$$\left(\vphantom{\hat{{\boldsymbol { C } }}+\hat{{\boldsymbol { K } }}^{-1}}\right. \hat{{\boldsymbol { C } }} \hat{{\boldsymbol { K } }}^{-1}_{} \left.\vphantom{\hat{{\boldsymbol { C } }}+\hat{{\boldsymbol { K } }}^{-1}}\right)^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }} & {\boldsymbol { 0 } } \end{bmatrix} \left(\vphantom{{\boldsymbol { C } }+ {\boldsymbol { K } }^{-1}}\right. \left.\vphantom{{\boldsymbol { C } }+ {\boldsymbol { K } }^{-1}}\right)^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }} & {\boldsymbol { 0 } } \end{bmatrix}^{T}_{}$$

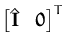to replace ($\hat{C}$ + $\hat{{\boldsymbol { K } }}^{-1}_{}$)^-1. The matrix [$\hat{{\boldsymbol { I } }}$  0] is the concatenation of the identity matrix of size N - 1 with a column of N - 1 zeroes. The replacement leads to

$$\hat{{\boldsymbol { \Lambda } }} \hat{{\boldsymbol { K } }}^{-1}_{} \hat{{\boldsymbol { K } }}^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix} \left(\vphantom{{\boldsymbol { C } }+ {\boldsymbol { K } }^{-1}}\right. \left.\vphantom{{\boldsymbol { C } }+ {\boldsymbol { K } }^{-1}}\right)^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix}^{T}_{} \hat{{\boldsymbol { K } }}^{-1}_{}$$ = (125)

$$\hat{{\boldsymbol { K } }}^{-1}_{} \hat{{\boldsymbol { K } }}^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix} \left[\vphantom{{\boldsymbol { K } }-{\boldsymbol { K } }\left({\... ...ymbol { C } }^{-1}+{\boldsymbol { K } }\right)^{-1}{\boldsymbol { K } }}\right. \left(\vphantom{{\boldsymbol { C } }^{-1}+{\boldsymbol { K } }}\right. \left.\vphantom{{\boldsymbol { C } }^{-1}+{\boldsymbol { K } }}\right)^{-1}_{} \left.\vphantom{{\boldsymbol { K } }-{\boldsymbol { K } }\left({\... ...ymbol { C } }^{-1}+{\boldsymbol { K } }\right)^{-1}{\boldsymbol { K } }}\right] \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix}^{T}_{} \hat{{\boldsymbol { K } }}^{-1}_{}$$ =

$$\hat{{\boldsymbol { K } }}^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix} \left(\vphantom{{\boldsymbol { C } }^{-1}+{\boldsymbol { K } }}\right. \left.\vphantom{{\boldsymbol { C } }^{-1}+{\boldsymbol { K } }}\right)^{-1}_{} \begin{bmatrix}\hat{{\boldsymbol { I } }}&{\boldsymbol { 0 } }\end{bmatrix}^{T}_{} \hat{{\boldsymbol { K } }}^{-1}_{}$$ =

$$\Lambda$$ = (126)

The product K  [$\hat{{\boldsymbol { I } }}$  0]  $\hat{{\boldsymbol { K } }}^{-1}_{}$ = P_N is an orthogonal projection in the feature space $\pmb$$\cal {F}$. The projection eliminates the last component by orthogonally projecting it to the span of the first N - 1 examples.

Next we consider the linear term in the EP-parametrisation of the GP from eq. (117) with respect to $\hat{{\boldsymbol { \Phi } }}^{T}_{}$f: $\Lambda$a. The sparse learning rules change it to $\hat{{\boldsymbol { \Lambda } }}$$\hat{{\boldsymbol { a } }}$ and the new value is obtained from changes in the natural parametrisation via eqs. (121) and (122). We use, similarly to the case for the quadratic term, the result from eq. (79) to relate the reduced and the full EP-parameters of the GP:

$$\begin{split}\hat{{\boldsymbol { \Lambda } }}\hat{{\boldsymbo... ... } }\end{bmatrix}^T \hat{{\boldsymbol { \alpha } }} \end{split}$$ (127)

where from line two to line three of the equation we replaced ($\hat{{\boldsymbol { C } }}$ + $\hat{{\boldsymbol { K } }}^{-1}_{}$) with the corresponding expression from eq. (79) using the old quantities. Similarly to the case of the update of $\hat{{\boldsymbol { \Lambda } }}$ we eliminate the pruned $\hat{{\boldsymbol { \alpha } }}$ using eq. (77):

$$\hat{{\boldsymbol { \Lambda } }} \hat{{\boldsymbol { a } }} \Lambda$$ (128)

where P_N is again the projection matrix from eq. (126). Substituting back the pruned coefficients and using $\hat{{\boldsymbol { \Phi } }}$ as the basis set, the projection matrix P_N is grouped with $\hat{{\boldsymbol { \Phi } }}$ and we have the EP-parametrisation of the sparse GP from eq. (123) as

$$\widehat{{\ensuremath{{\cal{GP}}}}}_{post}^{} \Lambda \propto \left\{\vphantom{-\frac{1}{2}\left[ {\boldsymbol { f } }^T{\bolds... ...dsymbol { \Phi } }}^T{\boldsymbol { f } }-{\boldsymbol { a } }) \right]}\right. {\textstyle\frac{1}{2}} \left[\vphantom{ {\boldsymbol { f } }^T{\boldsymbol { f } }+ ({\b... ...t{{\boldsymbol { \Phi } }}^T{\boldsymbol { f } }-{\boldsymbol { a } }) }\right. \hat{{\boldsymbol { \Phi } }}^{T}_{} \Lambda \hat{{\boldsymbol { \Phi } }}^{T}_{} \left.\vphantom{ {\boldsymbol { f } }^T{\boldsymbol { f } }+ ({\b... ...t{{\boldsymbol { \Phi } }}^T{\boldsymbol { f } }-{\boldsymbol { a } }) }\right] \left.\vphantom{-\frac{1}{2}\left[ {\boldsymbol { f } }^T{\boldsy... ...symbol { \Phi } }}^T{\boldsymbol { f } }-{\boldsymbol { a } }) \right]}\right\}$$

$$\propto \cal {GP} \prod_{i=1}^{N} \mathcal {N} \hat{\phi}_{i}^{T} \lambda_{i}^{}$$ (129)

This result says that by changing the feature vectors associated with the likelihoods, we can keep the diagonal structure of the second term. The index from the projection matrix P_N has been ignored since it is straightforward that if successive projection steps are used, the corresponding matrices multiply and we have, for each input example, the approximation of the feature space image using only the elements from $\hat{{\boldsymbol { \Phi } }}$: $\hat{\phi}_{i}^{}$ = $\hat{{\boldsymbol { \Phi } }}$p_i = $\sum_{j}^{}$$\phi_{j}^{}$p_ij with $\phi_{i}^{}$ being the i-th column of P. Similarly to the basic EP algorithm, the approximation $\hat{\phi}_{i}^{}$ is used for the projection in obtaining the one-dimensional random variable from eq. (110): u_i = $\hat{\phi}_{i}^{T}$f.

The important result in eq. (129) is that the sparse EP algorithm preserves the structure of the EP parametrisation, the KL-optimal pruning changes ``only'' the directions of projecting the approximating likelihoods, there are no modifications in $\alpha$ or $\Lambda$. This means that when iterating the pruning procedure we have to store the successive projections of all data: assuming a projection matrix, the ``update'' for it is P_new = PP_old.

The multiplication of the orthogonal projections might suggest that there is no need for memorising a large P. Indeed, removing the last element is done with P_N = K[$\hat{{\boldsymbol { I } }}$0]$\hat{{\boldsymbol { K } }}^{-1}_{}$. If we remove one more element we use the matrix P_{N - 1} = $\hat{{\boldsymbol { K } }}_{N}^{}$[$\tilde{{\boldsymbol { I } }}$0]$\tilde{{\boldsymbol { K } }}^{-1}_{}$ with $\tilde{{\boldsymbol { K } }}$ the Gram matrix containing N - 2 elements, then their multiplication gives P = K[$\hat{{\boldsymbol { I } }}$0][$\tilde{{\boldsymbol { I } }}$0]$\tilde{{\boldsymbol { K } }}^{-1}_{}$ and if we know the N - 2 elements of $\tilde{{\boldsymbol { \Phi } }}$ then it might be enough to store $\tilde{{\boldsymbol { K } }}^{-1}_{}$ as in the previous chapter. This is indeed the case if we do not add elements to $\cal {BV}$ set in between the removals. Otherwise we must know the content of the $\cal {BV}$ set when removing an element and keep track of the changes to this particular subset.

A first observation is that the storage of the projection matrix P is needed, increasing the memory requirements from $\cal {}$O(d²) to $\cal {O}$(Nd + d²) where d is the size of the $\cal {BV}$ set.

Secondly, we see that the KL-optimal pruning of a $\cal {BV}$ does not mean that the approximated likelihood for that data is constant: the direction of the projection is changed. In practise the successive projections might mean the effective removal of a likelihood term, but this is often not the case. The presence of the approximated likelihood even for data which have been removed might justify the good experimental results for the sparse online learning [19].

A third useful remark is the relation of the two GP-parametrisations in the sparse case. This is an obvious generalisation of the correspondence given in Section 4.3, eqns. (121) and (122) deduced for the non-sparse case:

$$\begin{split}{\boldsymbol { \alpha } }&= {\boldsymbol { P } }... ... } }\right)^{-1} + {\boldsymbol { K } }\right)^{-1} \end{split}$$ (130)

The difference from the non-sparse case is that, due to the sparsity, the lemma-based representation alone cannot provide the EP-representation, the system is under-determined. In practise, eqns. (130) were used to check the correctness of the implemented code.⁶.

To summarise, the expectation-propagation for the sparse GP implies the projection on a different direction of the random variable f in the feature space. The change of the term u_i from eq. (110) implies that the result of the subtraction of the approximated likelihood is different from eq. (116). If an example (x_i,y_i) is chosen, then first we have to subtract the approximated likelihood from the GP. The new parameters ($\tilde{{\boldsymbol { \mu } }}$,$\tilde{\ensuremath{{\boldsymbol { \Sigma } }}}$) are:

$$\begin{split}\tilde{{\boldsymbol { \mu } }} &= {\boldsymbol {... ... v_i {\boldsymbol { h } }_i{\boldsymbol { h } }_i^T \end{split} \begin{split}{\boldsymbol { h } }_i &= \ensuremath{{\boldsymb... ...i\ensuremath{{\boldsymbol { \Sigma } }}\hat{\phi}_i \end{split}$$ (131)

and translated into the parameters ($\alpha$,C), we have the corrections to these parameters required before applying the online updates as:

$$\begin{split}\tilde{{\boldsymbol { \alpha } }} &= {\boldsymbo... ...+ v_i{\boldsymbol { h } }_i{\boldsymbol { h } }_i^T \end{split} \begin{split}{\boldsymbol { h } }_i &= {\boldsymbol { C } }{\... ...l { C } }{\boldsymbol { K } }{\boldsymbol { p } }_i \end{split}$$ (132)

where K is the Gram matrix of the $\cal {BV}$ elements and p_i is i-th column of the projection matrix P.

Comparisons for regression

The sparse EP is a refinement of the sparse online algorithm, thus it is related to the kernel PCA methods [73] and the Nyström method proposed to speed up kernel machines [101]. In the following we compare the Nyström method applied for the regression case with the sparse EP algorithm.

The Nyström method uses the feature space $\pmb$$\cal {F}$and a subset from the training set to construct an approximation to the eigenvalues of the kernel function, presented in details in Section 3.7. Using a subset of size m, there will be only m nonzero approximated eigenfunctions. Assuming a data set of size N, the N×N kernel matrix K_N is approximated with the smaller-rank

$$\tilde{{\boldsymbol { K } }}_{N}^{}$$ (133)

where we used the projection matrix P = k_NmK_m^-1 from the previous section and we assumed that the subset of size m for the Nyström method is the $\cal {BV}$ set.

In applications the inversion of the large K_N is replaced with the inversion of the smaller matrix K_m and the matrix inversion lemma from eq. (181) is exploited to reduce the cost of computations. For regression, where we know the analytical result, the Nyström method applied to computing the predictive mean at x is

$$\langle \rangle_{NY}^{} \left(\vphantom{\sigma_0^2{\boldsymbol { I } }_N + \tilde{{\boldsymbol { K } }}_N}\right. \sigma_{0}^{2} \tilde{{\boldsymbol { K } }}_{N}^{} \left.\vphantom{\sigma_0^2{\boldsymbol { I } }_N + \tilde{{\boldsymbol { K } }}_N}\right)^{-1}_{} \left(\vphantom{\sigma_0^2{\boldsymbol { I } }_N + {\boldsymbol { P } }{\boldsymbol { K } }_{BV}{\boldsymbol { P } }^T}\right. \sigma_{0}^{2} \left.\vphantom{\sigma_0^2{\boldsymbol { I } }_N + {\boldsymbol { P } }{\boldsymbol { K } }_{BV}{\boldsymbol { P } }^T}\right)^{-1}_{}$$ (134)

where k_N = [K₀(x₁,x),..., K₀(x_N,x)]^T, $\sigma_{0}^{2}$ is the noise variance, and t_N is the vector of outputs.

To compare it with the sparse EP algorithm, we assume a specific order for the presentation of the data: the elements of the $\cal {BV}$ set are presented first and there is no removal. This is equivalent with applying the KL-projection to the full posterior process. For the full process we have $\Lambda$_N = I_N/$\sigma_{0}^{2}$ and a_N = t_N. We apply the KL-projection to the $\cal {BV}$ set, leading to the GP with parameters in the EP representation:

$$\begin{split}{\boldsymbol { \Lambda } }&= {\boldsymbol { P } ... ...}_N = {\boldsymbol { P } }^T {\boldsymbol { t } }_N \end{split}$$ (135)

and similarly we compute the predictive mean for the sparse EP algorithm: where k_BV = [K₀(x₁,x),..., K₀(x_m,x)]^T. We interpret Pk_BV as the reconstruction of k_N from eq. (134), and similarly PP^Tt_N is an approximation to t_N using the m available basis vectors. We write the expression corresponding to the predictive variance for the EP regression (using k^* = K₀(x,x)).

$$\sigma_{EP}^{2} \left(\vphantom{{\boldsymbol { P } }{\boldsymbol { k } }_{BV}}\right. \left.\vphantom{{\boldsymbol { P } }{\boldsymbol { k } }_{BV}}\right)^{T}_{} \left(\vphantom{\sigma^2_0{\boldsymbol { I } }_N + {\boldsymbol { P } }{\boldsymbol { K } }_{BV}{\boldsymbol { P } }^T}\right. \sigma^{2}_{0} \left.\vphantom{\sigma^2_0{\boldsymbol { I } }_N + {\boldsymbol { P } }{\boldsymbol { K } }_{BV}{\boldsymbol { P } }^T}\right)^{-1}_{}$$ (136)

We see again that the predictive variance is also expressed using the reconstructions of the inputs from the $\cal {BV}$ set. A similar construction for the predictive variance in the Nyström method does not exist: we do not get positives variance at all input points x, the Nyström method is probabilistically inconsistent, this is because it only considers the GP marginals at the data locations. Compared with the Nyström method, we see that the sparse EP algorithm provides a less accurate posterior mean then the Nyström method method, but it has the advantage of a fully probabilistic treatment.

The proposed algorithm

The algorithm proposed here has an increased complexity compared with the sparse online algorithm and the same structure as the original expectation-propagation [46]. Additional cost, compared with the sparse online algorithm arises from the need to update the P, the matrix of projections, that requires $\cal {O}$(Nd ) operations.

Similarly to the sparse online algorithm from Section 3.6, we set the maximal $\cal {BV}$ set size in advance to M$\cal {BV}$. Whenever the size of the $\cal {BV}$ set gets larger then M$\cal {BV}$ we delete the $\cal {BV}$ with the smallest score. For algorithmic stability we also use the tolerance value $\epsilon_{tol}^{}$ to prevent the Gram matrix from being singular.

It starts with initialising the GP parameters ($\alpha$,C) and $\cal {BV}$ set with empty values, and also initialising the EP parameters (a_i,$\lambda_{i}^{}$) for all inputs with zero values. Since $\cal {BV}$ set is empty, the projection matrix is also empty.

For a selected example (x_i,y_i) the algorithm iterates the following steps:

1. If $\lambda_{i}^{}$ > 0 then compute the correction for the GP using eqs. (116), i.e. subtract the contribution from the previous iterations.

2. Compute the online GP update coefficients r⁽ⁱ⁾, q⁽ⁱ⁾ using eq. (53), and $\gamma_{i}^{}$ using eq. (61) and perform the updates for the
   • GP parameters ($\alpha$,C) using eq. (57),

   • inverse Gram matrix Q, using eq. (64),

   • local EP parameters (a_i,$\lambda_{i}^{}$), based on eq. (114),

   • projection vector P by adding a new column containing e_i.

   If $\gamma_{i}^{}$ < $\epsilon_{tol}^{}$ then perform the sparse updates.

3. If the size of the $\cal {BV}$ set is larger than M$\cal {BV}$ then
   • compute the score for all elements of the $\cal {BV}$ set,

   • remove the minimal element from the
     • GP parameters ($\alpha$,C) using eqs. (78) and (80),
     • projection vector P_new.
     • inverse Gram matrix Q using eq. (81).

The algorithm is iterated until some convergence criterion is met or for a fixed number of sweeps through the whole data. In the experiments we employed the later choice. This seemed reasonable since a steady performance was reached in most cases after the second sweep through the data. A more detailed sketch of the algorithm is given in Appendix G, with related equations written explicitly.

Discussion and Further Research

This chapter developed an iterative approach to improve on the sparse online solution such that the sparseness, i.e. the possibility of a flexible treatment of the $\cal {BV}$ set size, is preserved.

The improvement is based on the expectation-propagation algorithm for the GPs, presented by [46]. Its extension to sparse GPs increases the computational demand by requiring, beyond the parameters (a_i,$\lambda_{i}^{}$), the storage of a projection matrix P of size N×d with d being the size of the $\cal {BV}$ set.

We believe that the EP algorithm for the sparse GPs fills in a gap in the applicability of GPs: if we have a small data set, then the EP algorithm proposed originally by [46] suffices. For the case of large datasets, we believe (as supported by experiments), that the sparse GP algorithm presented in Chapter 3 is the only available method if we want to use GPs. Additionally, there is a class of problems with data size that makes the EP algorithm inapplicable or inefficient, but for which the sparse online GP algorithm does not provide a sufficiently good solution. For these algorithms the EP extension of the sparse GPs can be used.

Further work needs to consider model selection for this class of algorithms. We have the ability to approximate the data likelihood, and this could provide us with an appropriate tuning of the hyper-parameters.

An interesting problem is the extensibility of the sparse framework to non-Gaussian families. This is suggested by the observation that if we use the EP-representation, then minimising the KL-divergence translates into simple projections of the examples to the set of basis vectors. Pruning is then performed by writing the solution of the problem into the EP-form of eq. (117), performing the removal of inputs in this framework and transforming back into a more convenient representation.