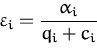The Sparse EP algorithm


Init. Choose the kernel type and parameters. Set the M$ \cal {BV}$ and $ \epsilon_{tol}^{}$.

Set the $ \cal {BV}$ set to empty set. Set ($ \alpha$,C), (a,$ \Lambda$,P), and (K,Q) to empty values.

t = 0
Iterate For a selected example (yt + 1,xt + 1) do
(a)
Par. adj. (EP)
If $ \lambda_{t+1}^{}$ $ \neq$ 0 then (subtract contribution from previous iteration)
ht + 1      

v_t+1^-1 = &lambda#lambda;_t+1^-1 - p ^T_t+1 K p _t+1 - p _t+1^T K C K p _t+1
#<19103#> &alpha#alpha; = &alpha#alpha; + h _t+1 v_t+1 ( &alpha#alpha; ^T K p _t+1 - a_t+1)
#<19115#> C = C + v_t+1 h _t+1 h _t+1^T
(b)
Online coeff.

Compute q(t + 1) and r(t + 1) using $ \cal {GP}$  with ($ \tilde{{\boldsymbol { \alpha } }}$,$ \tilde{{\boldsymbol { C } }}$), the first and second derivatives of:

ln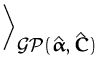$\displaystyle \bigg\langle$P(yt + 1|xt + 1, ft + 1)$\displaystyle \bigg\rangle_{\displaystyle {\ensuremath{{\cal{GP}}}}(\hat{{\boldsymbol { \alpha } }},\hat{{\boldsymbol { C } }})}^{}$    
(c)
Scalars & Vectors


k*t + 1 = K0(xt + 1,xt + 1)              

#<19156#> e _t+1 = Q k _t+1                          &gamma#gamma;_t+1 = k^*_t+1 - k _t+1^T#<19164#> e _t+1
&sigma#sigma;^2_t+1 = k^*_t+1 + k _t+1^T C k _t+1                          &eta#eta;_t+1 = (1 +&gamma#gamma;_t+1r^(t+1))^-1

(d)
EP update
at + 1      

&lambda#lambda;_t+1 = - ( (r^(t+1))^-1 + &sigma#sigma;_t+1^2 )^-1
(e)Geom. test If $ \gamma_{t+1}^{}$ < $ \epsilon_{tol}^{}$ then (perform full update)
st + 1      

p _t+1 = #<19186#> e _t+1 otherwise(perform sparse update)
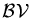  • add xt + 1 to the $ \cal {BV}$ set:
    Knew      

Q ^new = Q + &gamma#gamma;^-1_t+1 (#<19209#> e _t+1 - e _t+1)(#<19213#> e _t+1+ e _t+1)^T compute
st + 1      

p _t+1 = e _t+1 (where pi is the i-th row of matrix P.)
(f) $ \cal {GP}$  par. update
$\displaystyle \alpha$new      

C ^new = #<19245#> C + r^(t+1)&eta#eta;_t+1 s _t+1 s _t+1^T
(g) $ \cal {BV}$ removal If $\char93 \ensuremath{{\cal{BV}}}>M_\ensuremath{{\cal{BV}}}$ (remove a $ \cal {BV}$ )
  • compute scores for each $ \cal {BV}$ (i):

    \begin{displaymath} \ensuremath{\mathrm{\varepsilon}}_i = \frac{\alpha_i}{q_i + c_i} \end{displaymath}

  • find the $ \cal {BV}$ with minimal score $j = argmin \{\ensuremath{\mathrm{\varepsilon}}_i\vert i\in \ensuremath{{\cal{BV}}} \}$
  • remove $\ensuremath{{\cal{BV}}}_j$ from the BV set, using notation from Fig. 3.3 and Fig. D.1, with $ \cal {BV}$ set rearranged such that the j-th element is the last one.
    $\displaystyle \alpha$new      

C ^new = C ^(r) + Q ^* Q ^*Tq^* - ( Q ^*+ C ^*)( Q ^*+ C ^*)^T q^* + c^*
Q ^new = Q ^(r) - Q ^* Q ^*Tq^*
P ^new = P ^(r) - P ^* Q ^*Tq^* where P(r) is the matrix P without the j-th column (or the last one, if we reordered the $ \cal {BV}$ set), and P* is the column vector containing the projection coefficients corresponding to the j-th $ \cal {BV}$ element.
(h)Goto (a) t = t + 1

Select a new input (yt + 1,xt + 1) to process.

Restart iteration.

1

L CSATO 2003-04-23