Important: since it is quite technical, the text is mainly copy-pasted from the thesis (see References). For more compact information you can look at the Neural Computation article.

Online estimation of the posterior GP

The representation lemma shows that the posterior moments are expressed as linear and bilinear combinations of the kernel functions at the data points, allowing to tackle computationally the posterior process. On the other hand, the high-dimensional integrals needed for the coefficients q = [q1,..., qN]T and R = {Rij} of the posterior moments are rarely computable analytically, the parametrisation lemma thus is not applicable in practise and more approximations are needed.
The method used here is the online approximation to the posterior distribution using a sequential algorithm [55]. For this we assume that the data is conditionally independent, thus factorising
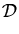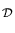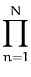P($\displaystyle \cal {D}$|f$\scriptstyle \cal {D}$) = $\displaystyle \prod_{n=1}^{N}$P(yn| fn,xn) (50)
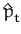
and at each step of the algorithm we combine the likelihood of a single new data point and the (GP) prior from the result of the previous approximation step [17,58]. If $ \hat{p}_{t}^{}$ denotes the Gaussian approximation after processing t examples, by using Bayes rule we have the new posterior process ppost given by
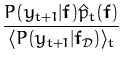
ppost(f) = $\displaystyle {\frac{P(y_{t+1}\vert{\boldsymbol { f } })\hat{p}_t({\boldsymbol { f } })}{\langle P(y_{t+1}\vert{\boldsymbol { f } }_{\cal D}) \rangle _t}}$ (51)
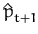
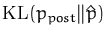
Since ppost is no longer Gaussian, we approximate it with the closest GP, $ \hat{p}_{t+1}^{}$ (see Fig. 2.2). Unlike the variational method, in this case the ``reversed'' KL divergence ${\ensuremath{\mathrm{KL}}}(p_{post}\Vert\hat{p})$ is minimised. This is possible, because in our on-line method, the posterior (51) only contains the likelihood for a single data and the corresponding non-Gaussian integral is one-dimensional. For many relevant cases these integrals can be performed analytically or we can use existing numerical approximations.

\includegraphics[]{online.eps}
Figure 2.2: Visualisation of the online approximation of the intractable posterior process. The resulting approximated process the from previous iteration is used as prior for the next one.
In order to compute the on-line approximations of the mean and covariance kernel Kt we apply the Parametrisation Lemma sequentially with a single likelihood term P(yt|ft,xt) at each step. Proceeding recursively, we arrive at
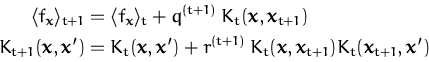
\begin{displaymath}\begin{split}\langle f_{\boldsymbol { x } } \rangle _{t+1} &=t({\boldsymbol { x } }_{t+1},{\boldsymbol { x } }') \end{split}\end{displaymath} (52)
where the scalars q(t + 1) and r(t + 1) follow directly from applying the Parametrisation Lemma 2.3.1 with a single data likelihood P(yt + 1|xt + 1, fxt + 1) and the process from time t:
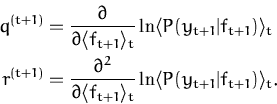
\begin{displaymath}\begin{split}q^{(t+1)} &= \frac{\partial}{\partial \langle f_... ..._t} \ln \langle P(y_{t+1}\vert f_{t+1}) \rangle _t. \end{split}\end{displaymath} (53)
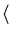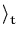
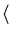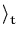
where ``time'' is referring to the order in which the individual likelihood terms are included in the approximation. The averages in (53) are with respect to the Gaussian process at time t and the derivatives taken with respect to $ \langle$ft + 1$ \rangle_{t}^{}$ = $ \langle$f (xt + 1)$ \rangle_{t}^{}$. Note again, that these averages only require a one dimensional integration over the process at the input xt + 1.
The online learning eqs. (52) in the feature space have the simple from [55]:
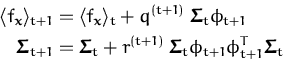
\begin{displaymath}\begin{split}\langle f_{\boldsymbol { x } } \rangle _{t+1} &=... ...phi_{t+1}^T\ensuremath{{\boldsymbol { \Sigma } }}_t \end{split}\end{displaymath} (54)
Unfolding the recursion steps in the update rules (52) we arrive at the parametrisation for the approximate posterior GP at time t as a function of the initial kernel and the likelihoods:
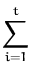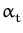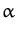$\displaystyle \langle$fx$\displaystyle \rangle_{t}^{}$ = $\displaystyle \sum_{i=1}^{t}$K0(x,xi)$\displaystyle \alpha_{t}^{}$(i) = $\displaystyle \alpha$tTkx (55)
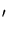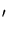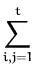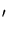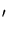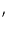
Kt(x,x$\scriptstyle \prime$) = K0(x,x$\scriptstyle \prime$) + $\displaystyle \sum_{i,j=1}^{t}$K0(x,xi)Ct(ij)K0(xj,x$\scriptstyle \prime$) = K0(x,x$\scriptstyle \prime$) + kxTCtkx$\scriptscriptstyle \prime$ (56)
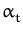
with coefficients $ \alpha_{t}^{}$(i) and Ct(ij) defining the approximation to the posterior process, more precisely to its coefficients q and R from the parametrisation and equivalently in eq. (48) using the feature space. The coefficients given by the parametrisation lemma and those provided by the online iteration eqs. (55) and (56) are equal in the Gaussian regression case only. The approximations are given recursively as
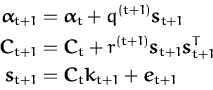
\begin{displaymath}\begin{split}{\boldsymbol { \alpha } }_{t+1} &= {\boldsymbol { k } }_{t+1} + {\boldsymbol { e } }_{t+1} \end{split}\end{displaymath} (57)
where kt + 1 = kxt + 1 = [K0(xt + 1,x1),..., K0(xt + 1,xt)]T and et + 1 = [0, 0,..., 1]T is the t + 1-th unit vector.

Observations

The likelihood function was left unspecified. The requirement for the online algorithm is the approximability of the scalar coefficients q(t+1) and r(t+1). Several likelihood functions have this property and the regression with Gaussian noise is the trivial example where the integral is exact. For regression with exponential noise the quantities are still computable. Several examples are presented later (Examples).
It is important that the online estimation increases the size of the parameters: the estimation of the posterior mean ultimately requiring all inputs to be stored and kernel producs to be computed. The increasing size of parameters severely restricts the applicability of the online estimation method to the non-parametric GPs. The sparse extension of the online algorithm tackles this drawback.

Questions, comments, suggestions: contact Lehel Csató.