Robust Regression with online Gaussian Processes

Robust regression is defined in this framework as function estimation from noisy data with additive, but non-gaussian noise. We present GP regression estimates fist assuming a heavy-tailed symmetric Laplace noise. A second example is when the noise is further ``worsened'' (from the estimation point of view): it is heavy-tailed and positive.

Two noise models, exponential but heavy-tailed, are presented. The first noise model has a symmetric Laplace distribution:

P_s(y| f_t+1, $\displaystyle \lambda$ ) = $\displaystyle {\frac{{\lambda}}{{2}}}$ exp $\displaystyle \left(\vphantom{ -\lambda\vert y-f_{t+1}\vert}\right.$ - $\displaystyle \lambda$ | y - f_t+1| $\displaystyle \left.\vphantom{ -\lambda\vert y-f_{t+1}\vert}\right)$

(1)

where $\lambda$ is the inverse of the noise variance, y is the observed noisy output, and f_t+1 is the latent output which is assumed to be a Gaussian random variable. The second model is a non-symmetric version where the noise can only be positive, thus the likelihood function is:

Given a likelihood function and implicitly a training input $({\ensuremath{\boldsymbol { x } }}_{t+1},y_{t+1})$ , to apply the online learning, we need to compute the average of this likelihood with respect to a one-dimensional Gaussian random variable $f_{t+1}\sim\ensuremath{{N}}(\mu_{t+1},\sigma^2_{t+1})$ where the Gaussian distribution is the marginal of the approximated GP at the location of the new input (see e.g. [4,2]). To obtain the update coefficients, we then need to compute the derivatives of the log-average with respect to the prior mean $\mu_{{t+1}}^{}$ .

Positive noise

First we compute the average likelihood for the non-symmetric noise model, eq. (2). We define the function g as this average:

g( $\displaystyle \mu_{{t+1}}^{}$ , $\displaystyle \sigma_{{t+1}}^{}$ , $\displaystyle \lambda$ ) = $\displaystyle \langle$ P_p(y| f_t+1, $\displaystyle \lambda$ ) $\displaystyle \rangle_{{\ensuremath{{N}}(\mu_{t+1},\sigma^2_{t+1})}}^{}$ = $\displaystyle \lambda$ exp $\displaystyle \left(\vphantom{ \theta\left( \frac{\theta}{2}-a\right)}\right.$ $\displaystyle \theta$ $\displaystyle \left(\vphantom{ \frac{\theta}{2}-a}\right.$ $\displaystyle {\frac{{\theta}}{{2}}}$ - a $\displaystyle \left.\vphantom{ \frac{\theta}{2}-a}\right)$ $\displaystyle \left.\vphantom{ \theta\left( \frac{\theta}{2}-a\right)}\right)$ $\displaystyle \Phi$ $\displaystyle \left(\vphantom{ -\theta+a }\right.$ - $\displaystyle \theta$ + a $\displaystyle \left.\vphantom{ -\theta+a }\right)$

(3)

a = $\displaystyle {\frac{{\mu_{t+1}-y}}{{\sigma_{t+1}}}}$ , $\displaystyle \theta$ = $\displaystyle \lambda$ $\displaystyle \sigma_{{t+1}}^{}$ , and $\displaystyle \Phi$ (z) = $\displaystyle \int_{{-\infty}}^{z}$ exp $\displaystyle \left(\vphantom{-\frac{t^2}{2}}\right.$ - $\displaystyle {\frac{{t^2}}{{2}}}$ $\displaystyle \left.\vphantom{-\frac{t^2}{2}}\right)$ $\displaystyle {\frac{{dt}}{{\sqrt{2\pi}}}}$ .

(4)

Note that the pair of parameters ( $\theta$ , a) is enough for parametrising g since the noise parameter $\lambda$ is fixed in this derivation, Thus, in the following we will use g( $\theta$ , a) and use $\partial_{a}^{}$ f = $\partial_{\mu}^{}$ f / $\sigma_{{t+1}}^{}$ , result of the definition of a.

We have the update coefficient q^(t+1) for the posterior mean function based on the new data $({\ensuremath{\boldsymbol { x } }},y)$ as:

q^(t+1) = $\displaystyle \partial_{{\mu_{t+1}}}^{}$ log g( $\displaystyle \theta$ , a) = - $\displaystyle \lambda$ + $\displaystyle {\frac{{\lambda}}{{\theta\sqrt{2\pi}}}}$ $\displaystyle {\frac{{\exp\left(-\frac{(\theta -a)^2}{2}\right)}}{{\Phi(-\theta + a)}}}$

(5)

r^(t+1) = $\displaystyle \partial^{2}_{{\mu_{t+1}}}$ log g( $\displaystyle \theta$ , a) = $\displaystyle {\frac{{\displaystyle \partial^2_{\mu_{t+1}} g(\theta,a)}}{{g(\theta,a)}}}$ - $\displaystyle \left(\vphantom{q^{(t+1)}}\right.$ q^(t+1) $\displaystyle \left.\vphantom{q^{(t+1)}}\right)^{2}_{}$

(6)

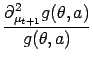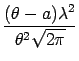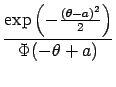$\displaystyle {\frac{{\partial^2_{\mu_{t+1}} g(\theta,a)}}{{g(\theta,a)}}}$ = $\displaystyle \lambda^{2}_{}$ - $\displaystyle {\frac{{(\theta - a)\lambda^2}}{{\theta^2\sqrt{2\pi}}}}$ $\displaystyle {\frac{{\exp\left(-\frac{(\theta -a)^2}{2}\right)}}{{\Phi(-\theta + a)}}}$

When applying online learning, we iterate over the inputs $[({\ensuremath{\boldsymbol { x } }}_1,y_1),\ldots,({\ensuremath{\boldsymbol { x } }}_N,y_N)]$ , at time t < N having an estimate of the GP marginal as a normal distribution $\ensuremath{{N}}(\mu_{t+1},\sigma^2_{t+1})$ and computing (q^(t+1), r^(t+1)) based on eqs. (5) and (6).

Symmetric noise

The update coefficients for the symmetric noise are obtained similarly to the positive case, based on the following averaged likelihood:

$\displaystyle \langle$ P_s(y| f_t+1, $\displaystyle \lambda$ ) $\displaystyle \rangle_{{\ensuremath{{N}}(\mu_{t+1},\sigma^2_{t+1})}}^{}$ = $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \bigg($ g( $\displaystyle \theta$ , a) + g( $\displaystyle \theta$ , - a) $\displaystyle \bigg)$ .

(7)

Repeating the deduction from the positive noise case, we have the first and second derivatives as

q^(t+1)	=	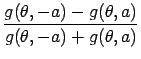$\displaystyle \lambda$ $\displaystyle {\frac{{g(\theta,-a) - g(\theta,a)}}{{g(\theta,-a)+g(\theta,a)}}}$
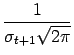r^(t+1)	=	$\displaystyle \lambda^{2}_{}$ $\displaystyle \left[\vphantom{ 1 - \frac{1}{\sigma_{t+1}\sqrt{2\pi}}\exp\left(-\frac{a^2}{2}\right) \frac{1}{g(\theta,-a)+g(\theta,a)} }\right.$ 1 - $\displaystyle {\frac{{1}}{{\sigma_{t+1}\sqrt{2\pi}}}}$ exp $\displaystyle \left(\vphantom{-\frac{a^2}{2}}\right.$ - $\displaystyle {\frac{{a^2}}{{2}}}$ $\displaystyle \left.\vphantom{-\frac{a^2}{2}}\right)$ $\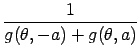displaystyle {\frac{{1}}{{g(\theta,-a)+g(\theta,a)}}}$ $\displaystyle \left.\vphantom{ 1 - \frac{1}{\sigma_{t+1}\sqrt{2\pi}}\exp\left(-\frac{a^2}{2}\right) \frac{1}{g(\theta,-a)+g(\theta,a)} }\right]$ - $\displaystyle \bigg($ q^(t+1) $\displaystyle \bigg)^{2}_{}$

Numerical problems

The above equations need to estimate the logarithm of the error function ( $\ensuremath{\mathrm{Erf}}$ ), which can be very unstable. In coding the Matlab implementation of the robust regression, an asymptotic expansion was used whenever the direct estimation of the $\log\ensuremath{\mathrm{Erf}}$ function became numerically unstable. See the Matlab code for details [3].

Changing the likelihood parameters

Since all models are exponential, we can adapt the likelihood parameters. This is a multi-step procedure and it takes place after the online iterations: it assumes that there is an approximation to the posterior GP (obtained with fixed likelihood parameters). This is the E-step from the EM algorithm [1,5].

In the M-step we maximise the following lower-bound to the marginal likelihood (model evidence):

which again involves only one-dimensional integrals (i.i.d. data were assumed), which leads to the following values for the likelihood parameters:

$\displaystyle {\frac{{N}}{{\lambda_p}}}$	=	$\displaystyle \sum_{{n=1}}^{N}$ $\displaystyle \langle$ H(y_n - f_n) $\displaystyle \rangle_{{\ensuremath{{N}}(\mu_n,\sigma^2_n)}}^{}$
$\displaystyle {\frac{{N}}{{\lambda_s}}}$	=	$\displaystyle \sum_{{n=1}}^{N}$ $\displaystyle \langle$ \| y_n - f_n\| $\displaystyle \rangle_{{\ensuremath{{N}}(\mu_n,\sigma^2_n)}}^{}$

Examples

In the following the regression with robust models is demonstrated on a toy example: the estimation of the noisy $\ensuremath{\mathrm{sinc}}$ function.

The estimation was compared with Gaussian noise assumption, thus involving three models for the likelihood function for which we can estimate the noise (see the EM algorithm from the previous section). See figure captions for more explanation.

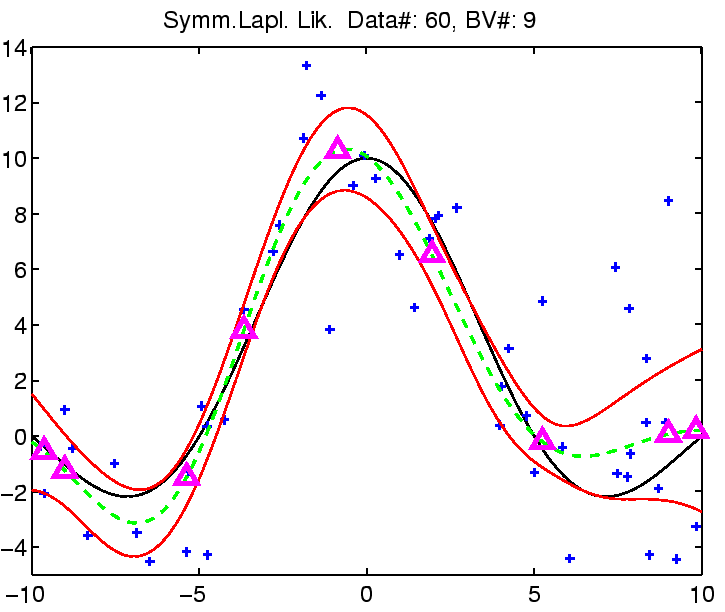
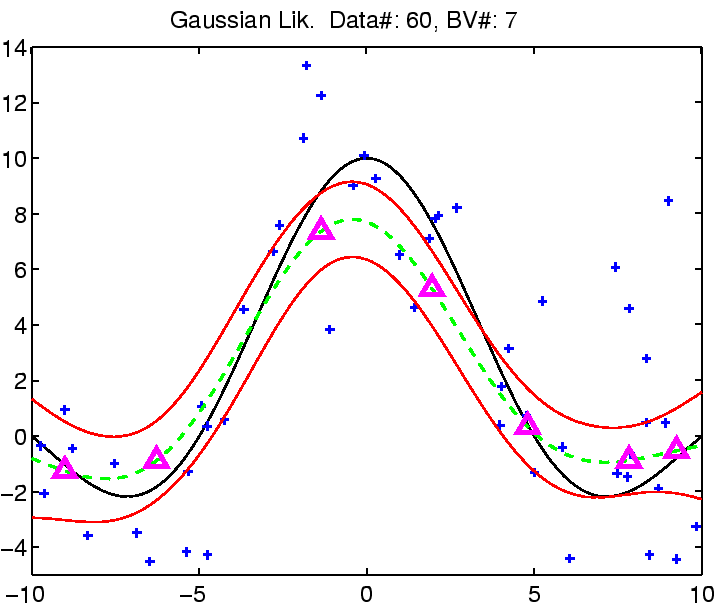
$\includegraphics{ex_reg_lapl_0.3-lapl_0.29.eps}$	$\includegraphics{ex_reg_lapl_0.3-gauss_26.eps}$
(a)	(b)

Figure 1: Comparing regression estimates with symmetric Laplace (a) and Gaussian (b) likelihoods. The true noise is symmetric Laplace ( $\lambda$ = 0.3). The algorithm estimates the length-scale and amplitude of the GP kernel (model parameters) and the noise of the likelihood. Subfigure (a): regression estimation with the true noise model. The error bars are the Bayesian error bars, specifying the variation of the latent variables which cannot be directly translated into error bars on the outputs y: the outputs have heavy tails. Subfigure (b): regression estimation with Gaussian noise assumption. With approximately the same and amplitude of the GP kernel function (determined using training), the noise estimation is $\sigma_{0}^{2}$ $\approx$ 35 which is a crude over-estimation of the actual variance of the outputs.

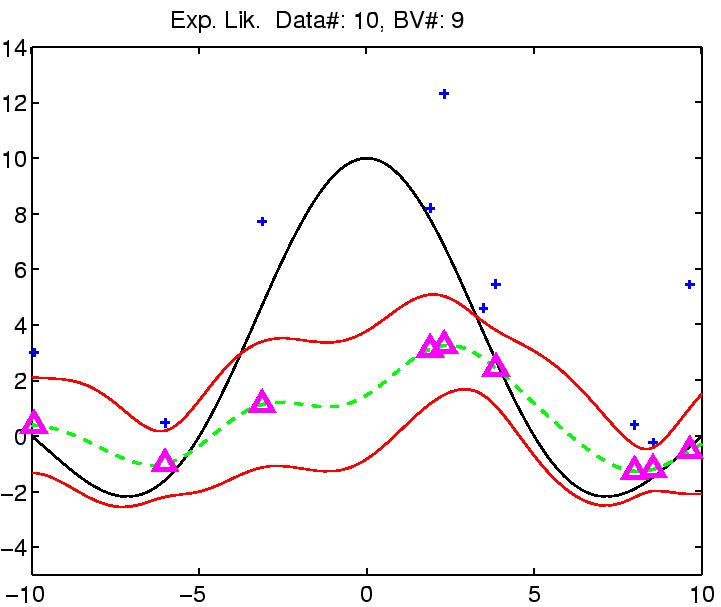
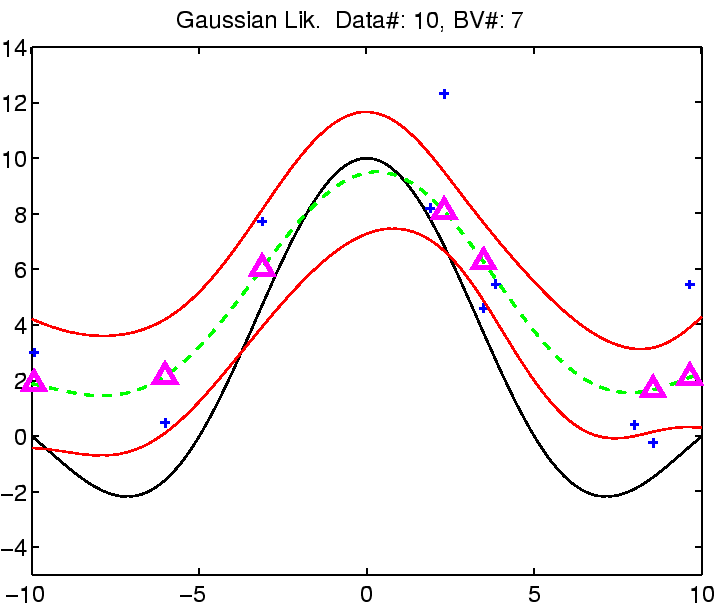
$\includegraphics{ex_reg_pos_0.4-pos_0.26.eps}$	$\includegraphics{ex_reg_pos_0.4-gauss_10.eps}$
(a)	(b)
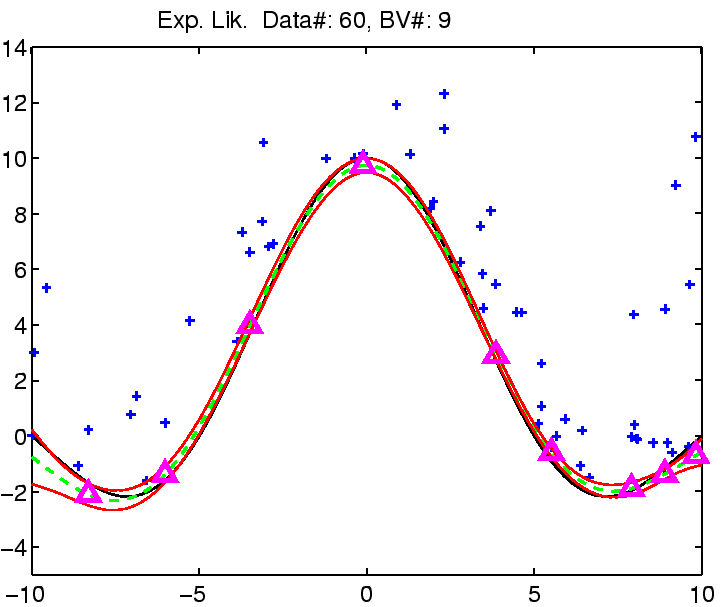
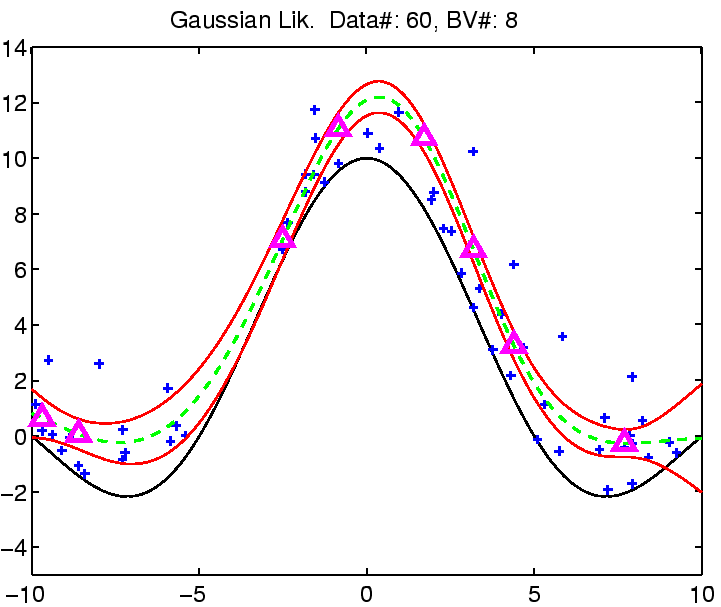
$\includegraphics{ex_reg_pos_0.4-pos_0.37_60.eps}$	$\includegraphics{ex_reg_pos_0.4-gauss_3_60.eps}$
(c)	(d)

Figure 2: Comparing regression estimates with positive exponential (a) and Gaussian (b) likelihoods. The true noise is a positive exponential ( $\lambda$ = 0.4). Similarly to Fig. 1, the algorithm estimates the length-scale and amplitude of the GP kernel (model parameters) and the noise of the likelihood. Subfigure (a): regression estimation with the true noise model. The error bars are the Bayesian error bars, specifying the variation of the latent variables which cannot be directly translated into error bars on the outputs y: the outputs have heavy tails. Subfigure (b): regression estimation with Gaussian noise assumption. With approximately the same and amplitude of the GP kernel function (determined by the training procedure), the noise estimate is $\sigma_{0}^{2}$ $\approx$ 3. Subfigures (c) and (d): the regression functions for more data, which allows more exact estimation of the true function. Notice that the Bayesian uncertainty for the correct model (left) shrinks more, reflecting more evidence.