The following property of the Gaussian probability density functions
(pdfs) is often used in this paper, here we state it in a form of a
theorem:
Theorem 1
Let
x 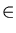
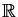 m
m and
p(
x) zero-mean Gaussian pdf with
covariance
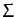
= {
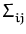
} (
i,
j from 1 to
m). If
g :
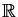 m
m 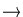
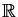
is a differentiable function
not growing faster than a polynomial and with partial derivatives
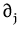 g
g(
x) =
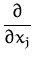 g
g(
x) ,
then
 dxp(x) xig(x) = dxp(x) xig(x) = 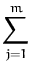 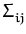  dxp(x) dxp(x) 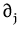 g(x) . g(x) . |
(185) |
In the following we will assume definite integration over
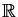 m
m whenever the integral appears. Alternatively, using the vector
notation, the above identity reads:
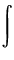 dxp(x) xg(x) = dxp(x) xg(x) = 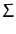 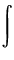 dxp(x) dxp(x) 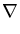 g(x) g(x) |
(186) |
For a general Gaussian pdf with mean
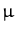
the above equation
transforms to:
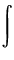 dxp(x) xg(x) = dxp(x) xg(x) = 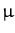 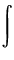 dxp(x) g(x) + dxp(x) g(x) + 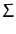 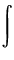 dxp(x) dxp(x) 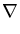 g(x) g(x) |
(187) |
Proof.
The proof uses the partial integration rule:
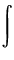 dxp(x) dxp(x)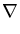 g(x) = - g(x) = - 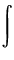 dxg(x) dxg(x)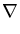 p(x) p(x) |
|
where we have used the fast decay of the Gaussian function to
dismiss one of the terms.
Using the derivative of a Gaussian pdf. we have:
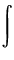 dxp(x) dxp(x)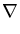 g(x) = g(x) = 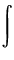 dx g(x) dx g(x)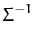 xp(x) xp(x) |
|
Multiplying both sides with
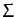
leads to
eq. (
186), completing the proof. For the nonzero mean
the deductions are also straightforward.
