Important: since it is quite technical, some text is mainly copy-pasted from the thesis (see References). For more compact information you can look at the Neural Computation article.

Sparse OGP Classification

Binary classification is not tractable analytically. But if on uses the probit model [49] where a binary value y $ \in$ { - 1, 1} is assigned to an input x $ \in$ $ \mathbb {R}$m with the data likelihood
P$\displaystyle \left(\vphantom{y\vert{\boldsymbol { f } }_{\boldsymbol { x } }}\right.$y|fx$\displaystyle \left.\vphantom{y\vert{\boldsymbol { f } }_{\boldsymbol { x } }}\right)$ = Erf$\displaystyle \left(\vphantom{\frac{y\; {\boldsymbol { f } }_{\boldsymbol { x } }}{\sigma_0}}\right.$$\displaystyle {\frac{y\; {\boldsymbol { f } }_{\boldsymbol { x } }}{\sigma_0}}$$\displaystyle \left.\vphantom{\frac{y\; {\boldsymbol { f } }_{\boldsymbol { x } }}{\sigma_0}}\right)$, (142)

where $ \sigma_{0}^{}$ is the noise variance and $\ensuremath{\mathrm{Erf}}(z)$ is the cumulative Gaussian distribution:
Erf(z) = $\displaystyle {\frac{1}{\sqrt{2\pi}}}$$\displaystyle \int^{z}_{-\infty}$dt  exp$\displaystyle \left(\vphantom{-\frac{t^2}{2}}\right.$ - $\displaystyle {\frac{t^2}{2}}$$\displaystyle \left.\vphantom{-\frac{t^2}{2}}\right)$ (143)

The shape of this likelihood resembles a sigmoidal, the main benefit of this choice is that its average with respect to a Gaussian measure is computable. We can compute the predictive distribution at a new example x:
p(y|x,$\displaystyle \alpha$,C) = $\displaystyle \langle$P(y|fx)$\displaystyle \rangle_{t}^{}$ = Erf$\displaystyle \left(\vphantom{\frac{y\; \langle {\boldsymbol { f } }_{\boldsymbol { x } } \rangle _t }{\sigma_x}}\right.$$\displaystyle {\frac{y\; \langle {\boldsymbol { f } }_{\boldsymbol { x } } \rangle _t }{\sigma_x}}$$\displaystyle \left.\vphantom{\frac{y\; \langle {\boldsymbol { f } }_{\boldsymbol { x } } \rangle _t }{\sigma_x}}\right)$ (144)

where $ \langle$fx$ \rangle_{t}^{}$ = kxT$ \alpha$ is the mean of the GP at x and $ \sigma_{\boldsymbol { x } }^{2}$ = $ \sigma_{0}^{2}$ + k*x + kxTCkx. It is the predictive distribution of the new data, that is the Gaussian average of an other Gaussian. The result is obtained by changing the order of integrands in the Bayesian predictive distribution eq. (143) and back-substituting the definition of the error function.
Based on eq. (53), for a given input-output pair (x, y) the update coefficients q(t + 1) and r(t + 1) are computed by differentiating the logarithm of the averaged likelihood from eq. (145) with respect to the mean at xt + 1 [17]:
q(t + 1) = $\displaystyle {\frac{y}{\sigma_{\boldsymbol { x } }}}$$\displaystyle {\frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}}}$                    r(t + 1) = $\displaystyle {\frac{1}{\sigma^2_{\boldsymbol { x } }}}$$\displaystyle \left\{\vphantom{\frac{\ensuremath{\mathrm{Erf}}''}{\ensuremath{\......\frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}} \right)^2 }\right.$$\displaystyle {\frac{\ensuremath{\mathrm{Erf}}''}{\ensuremath{\mathrm{Erf}}}}$ - $\displaystyle \left(\vphantom{\frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}} }\right.$$\displaystyle {\frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}}}$$\displaystyle \left.\vphantom{\frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}} }\right)^{2}_{}$$\displaystyle \left.\vphantom{\frac{\ensuremath{\mathrm{Erf}}''}{\ensuremath{\m......frac{\ensuremath{\mathrm{Erf}}'}{\ensuremath{\mathrm{Erf}}} \right)^2 }\right\}$ (145)

with $\ensuremath{\mathrm{Erf}}(z)$ evaluated at z = $ {\frac{y\;{\boldsymbol { \alpha } }_t^T{\boldsymbol { k } }_{x}}{\sigma_x}}$ and $\ensuremath{\mathrm{Erf}}'$ and $\ensuremath{\mathrm{Erf}}''$ are the first and second derivatives at z.
A more detailed description of the classifiaction framework is given in the THESIS (see References), or in the Neural Computation article.
Direct link to the section discussing classification from the thesis.

Classification Demo

The program ( demogp_class_gui) illustrates the Sparse OGP inference for binary classification. This demonstration program can fully be controlled using the buttons provided.
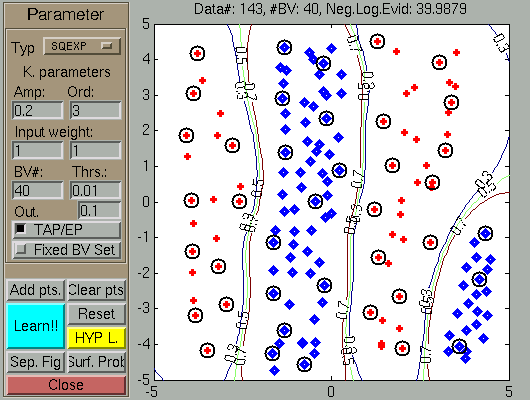
Classification GUI - initial stage
After the data addition (using the Add.Pts and the mouse), the GP LEARNS the classification boundary, shown in the figure with green line. Note that since no hyperparameter learning has been performed, the number of Basis Vectors (black circles on the figure) is quite large.
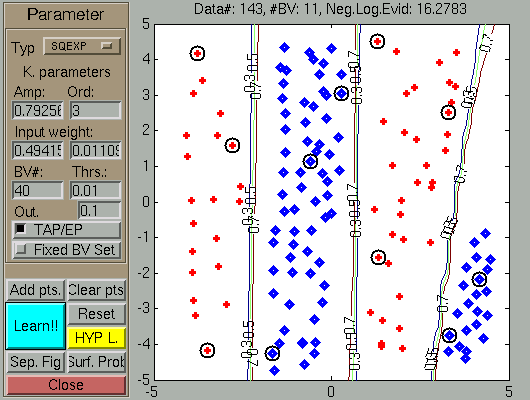
Classification GUI - final stage
The result of a fair amount of clicking (called data generation) and pressing the Learning -- Hyp.opt button pair is shown below. Observe that as a results of learning the scaling factors changed so that the first coordinate (X-axis) became more important than the second component, and the negative log-evidence is much reduced.
In the next figures we show the effect of flipping the coordinates whilst keeping the GP and the labels of the inputs.
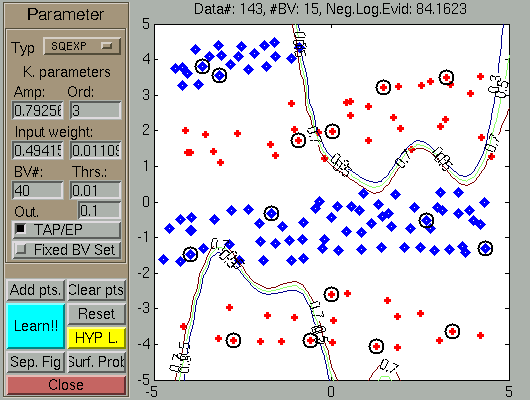
Classification GUI - flipped initial stage
The result of changing the coordinate order. The GP is not able to learn (which is not surprising) the classification boundary.
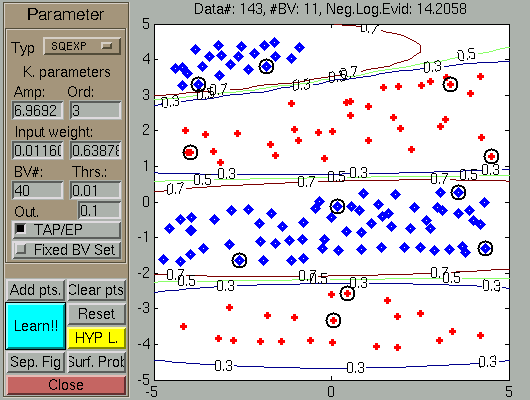
Classification GUI - flipped final stage
Applying several learning (Learning -- Hyp.opt) steps, the new configuration is the mirror of the earlier final result.

Questions, comments, suggestions: contact Lehel Csató.