Lecture 8 - Advanced parallel algorithms

Advanced recursive decomposition

Sometimes, recursive decomposition can be done more efficiently in a way in which the parts are not straightforward, but reduce the number of operations.

Basic example of such decomposition: compute a complex product by using only 3 (instead of 4) real multiplications).

Solution: (a+bi)*(c+di) = (ac-bd) + (ad+bc)i = (ac-bd) + (ac+ad+bc+bd-ac-bd)i = (ac-bd) + ((a+b)*(c+d) - ac - bd)i, which can be computed using only 3 real multiplications (but more additions/substractions).

Polynomial multiplication using Karatsuba algorithm

Note: for the classical algorithm, computing the coefficients leads to computing the products and then add diagonals in the following table:

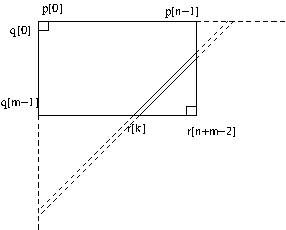
Idea:

• Split each of the input polynomials in half;
• Instead of multiplying each of the 4 pairs from the step above, use a similar trick to make only 3 multiplications

Assume input polynomials P(X) and Q(X) of degree 2*n-1.

Write them as P(X) = P₁(X)*X^n+P₂(X) and Q(X) = Q₁(X)*X^n+Q₂(X).

Now P(X)*Q(X) = (P₁(X)*X^n+P₂(X)) * (Q₁(X)*X^n+Q₂(X)) =
= P₁(X)* Q₁(X)*X^2n + (P₁(X)*Q₂(X)+P₂(X)*Q₁(X))*X^n + P₂(X)*Q₂(X)

But the second term can be written as
(P₁(X)+P₂(X)) * (Q₁(X)+Q₂(X)) - ₁(X)* Q₁(X) - P₂(X)*Q₂(X)

Notes:

• Complexity is Θ(n^log_2(3))
• While asymptotic complexity is better, Karatsuba's algorithm is quite complicated, so, the constant behind the Θ notation is way larger. This means that Karatsuba is better that the classical algorithm only for large enough polynomials.

Issues regarding recursive decomposition

• If threads are created explicitly, there needs to be a mechanism to stop creating threads at a certain depths or after creating a certain number of threads. Otherwise, the cost of creating threads eventually exceeds the cost of the actual operations.
• If thread pools are used, care needs to be taken to avoid having a deadlock situation where threads in the pool are waiting on tasks at deeper level in the tree, while those tasks are enqueued on the thread pool, but don't get threads to run on.