Important: since it is quite technical, some text is mainly copy-pasted from the thesis (see References). For more compact information you can look at the Neural Computation article.

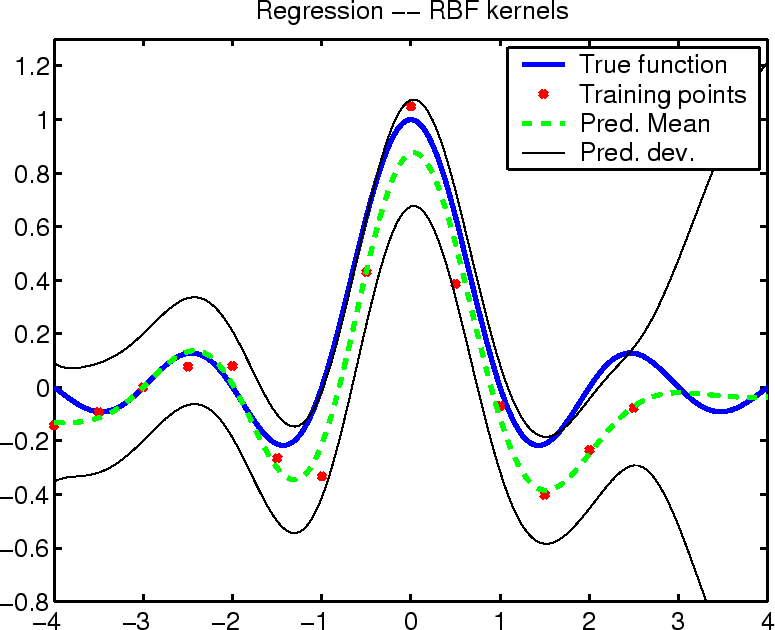
Regression with additive Gaussian noise

A trivial example of the above procedure is regression with additive Gaussian noise assumption. The image below shows the resulting mean of the posterior process together with the true function and the predicted variance around the mean.

Let us assume that the additive Gaussian noise has variance $\sigma_{0}^{2}$ . At time t + 1 we need the marginal of GP ( $\alpha$ _t,C_t) taken at the new data point x_{t + 1}. This marginal is a normal distribution with mean m_{t + 1} = k_{t + 1}^T $\alpha$ _t and covariance $\sigma_{t+1}^{2}$ = k^* + k_{t +
1}^TC_tk_{t + 1}. The coefficients q^{(t + 1)} and r^{(t +
1)} are :

An example of GP inference: learning the noisy sinc function. (click here to see the explanatory section from the thesis)

Exact computation, as it has been mentioned is only possible for the case above. The online approximation is be employed for non-standard regression where the noise is additive but the noise distribution is non-Gaussian.

For this exact case of regression with Gaussian noise one can show that the iterative online update is actually the iterative matrix inversion formula (presented in detail in Appendix C of the thesis).

Questions, comments, suggestions: contact Lehel Csató.