Important: since it is quite technical, some text is mainly copy-pasted from the thesis (see References). For a concise introduction look at Csato, Conford, Opper (2001).

Data Assimilation with sparse GPs

The PDF version of this document can be found here.
 
Inferring wind-fields from remote observations poses two issues that need to be tackled: the first one is to represent two-dimensional Gaussian fields, or processes (for each location we have random variables specifying the X-, and Y-directions.
The second problem is the inference with the inherently non-tractable likelihood model, governed by the underlying physics governing the wave formation and light reflection from water surfaces.

Inference with Vector Gaussian processes

Due to the pair of Gaussian random variables z at each location, the kernel function W0(x,y) is a 2×2 matrix, specifying the pairwise cross-correlation between the components at different spatial positions (notice that the notation of the kernel function is different). In the following z denotes the random vector corresponding to the wind-field at a single position and where $ \underline{{\boldsymbol { z } }}$ = [z1,...,zN]T denotes the concatenation of the local wind field components zi. These components are random variables corresponding to a spatial location xi. These locations specify the prior covariance matrix for the vector $ \underline{{\boldsymbol { z } }}$, given by W0 = {W0(xi,xj)}ij = 1N. The two-dimensional Gaussian p0 is the prior GP marginalised at zi, with zero-mean and covariance W0i.

In order to have a global model from the N, we combine them with a zero-mean vector GP [13,47]:

q($\displaystyle \underline{{\boldsymbol { z } }}$) $\displaystyle \propto$ $\displaystyle \left(\vphantom{\prod_{i}^N p({\boldsymbol { s } }_i\vert{\boldsymbol { z } }_i)}\right.$$\displaystyle \prod_{i}^{N}$p(si|zi)$\displaystyle \left.\vphantom{\prod_{i}^N p({\boldsymbol { s } }_i\vert{\boldsymbol { z } }_i)}\right)$p0($\displaystyle \underline{{\boldsymbol { z } }}$|W0)
where si is the vector of local observations at spatial location xi and zi is the corresponding vector of random variables.
The representation of the posterior GP thus requires vector quantities: the marginal of the vector GP at a spatial location x (and y for the covariance) has a bivariate Gaussian distribution with mean and covariance function of zx $ \in$ $ \mathbb {R}$2 represented as:
\begin{displaymath}\begin{split}\langle {\boldsymbol { z } }_{\boldsymbol { x } ... } }_0({\boldsymbol { x } }_j,{\boldsymbol { y } }) \end{split}\end{displaymath} (170)

where $ \alpha$z(1),$ \alpha$z(2),...,$ \alpha$z(N) and {Cz(ij)}i, j = 1, N are the coefficients of the vector GP describing the posterior mean and variance respectively. Although technical details, the quantities in are not scalars, one has to ``re-shuffle'' the expression in eq. (170).

Notice that this is exactly the same representation as for the scalar random variables, but due to the coupling in the likelihood model we have coupling in the representation of the posterior also.
Again, as with other likelihood models, in order to have a representation to the posterior, one has to compute the average of the likelihood p(si|zi). The different methods of performing the inference are detailed next.

Dealing with the likelihood

The likelihood is complex non-Gaussian and non-linearly dependent of the wind-direction. In the simplest case we assume that the scatterometer reads the output of a known nonlinear transformation but this output is corrupted by non-gaussian noise. Either the nonlinearity or the non-gaussianity make the posterior process non-tractable analytically. We present methods to approximate this non-tractable model.

Local inverse model:

Instead of using the direct likelihood p(si|zi), we transform eq. (170) using Bayes theorem to obtain the following expression for the posterior:

q($\displaystyle \underline{{\boldsymbol { z } }}$) $\displaystyle \propto$ $\displaystyle \left(\vphantom{\prod_{i}^N \frac{p_m({\boldsymbol { z } }_i\vert... ... s } }_i)} {p_0({\boldsymbol { z } }_i\vert{\boldsymbol { W } }_{0i})} }\right.$$\displaystyle \prod_{i}^{N}$$\displaystyle {\frac{p_m({\boldsymbol { z } }_i\vert{\boldsymbol { s } }_i,{\bo... ...dsymbol { s } }_i)}{p_0({\boldsymbol { z } }_i\vert{\boldsymbol { W } }_{0i})}}$$\displaystyle \left.\vphantom{\prod_{i}^N \frac{p_m({\boldsymbol { z } }_i\vert... ... s } }_i)} {p_0({\boldsymbol { z } }_i\vert{\boldsymbol { W } }_{0i})} }\right)$p0($\displaystyle \underline{{\boldsymbol { z } }}$|W0) (169)
where a mixture density network (MDN) [4] is used to model the conditional dependence of the local wind vector zi = (ui, vi) on the local scatterometer observations si:
pm(zi|si,$\displaystyle \omega$) = $\displaystyle \sum_{j=1}^{4}$$\displaystyle \beta_{ij}^{}$$\displaystyle \phi$(zi|cij,$\displaystyle \sigma_{ij}^{}$) (168)

where $ \omega$ is the union of the MDN parameters: for each observation at location xi we have the weightings $ \beta_{ij}^{}$ for the local Gaussians $ \phi$(cij,$ \sigma_{ij}^{2}$) where cij is the mean and $ \sigma_{ij}^{2}$ is the variance. The parameters of the MDN are determined using an independent training set [22] and are considered known in this section. The prior GP, which also has a set of hyper-parameters, was tuned carefully to represent features seen in real wind fields and is also known here.

This method of dealing with likelihoods was presented in the Wind-Field estimation section from the thesis (click here to see it).
Forward models
Here the forward wind-field to scatterometer mapping was learned using a truncated Fourier series for the scatterometer values and the coefficients of the Fourier series were the outputs of RBF networks whose inputs are the relative wind direction (to the satellite) and the incidence angle.
A gaussian noise model was assumed and a Taylor expansion of the RBF networks has been made, obtaining an approximation to the log-average.
The problem with this model is that it does not have a meaningful approximation for low wind-speeds, thus there has to be an initial small wind-direction.
For details look in (Cornford et.al. 2003).
Sampling from the local posterior
This approach also used the inferred Fourier series about the forward models from batch training, but rather than doing a Taylor expansion of the RBF functions in the likelihood, it used importance sampling instead.
The update coefficients were computed from the sampling mean and covariances of the resulting local posterior approximation.

Results

The results of the above methods were roughly similar, but their stability was different. Due to the local symmetries present in the model -- opposite wind-fields tend to produce very similar waves -- there are several local minima in which the inference can get trapped.
The forward model, if used with a zero-mean prior Gaussian process, gave inconsistent solutions, thus several restarts were needed. The solutions of the remaining two models were fairly consistent.
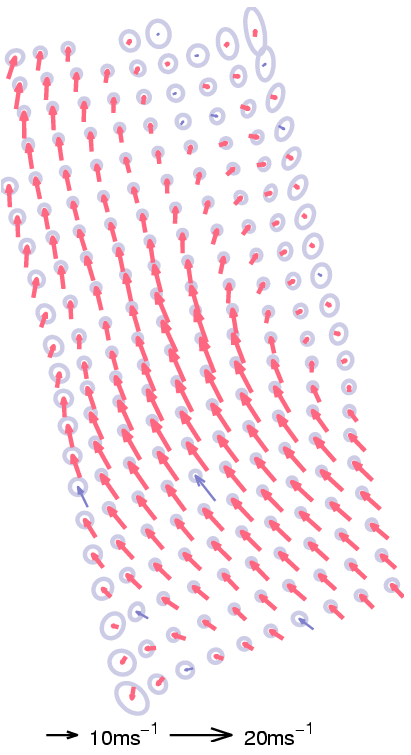
Posterior wind-fields and uncertainties - high number of BVs     Posterior wind-fields and uncertainties - small number of BVs
Figure 1. The results of the direct inverse model. The left sub-figure shows the inference when the GP representation was kept intact (189 in this case) and this is to be contrasted with the right sub-figure where only 38 BVs gave the same mean function, but with higher posterior uncertainty, illustrated with larger ellipses.
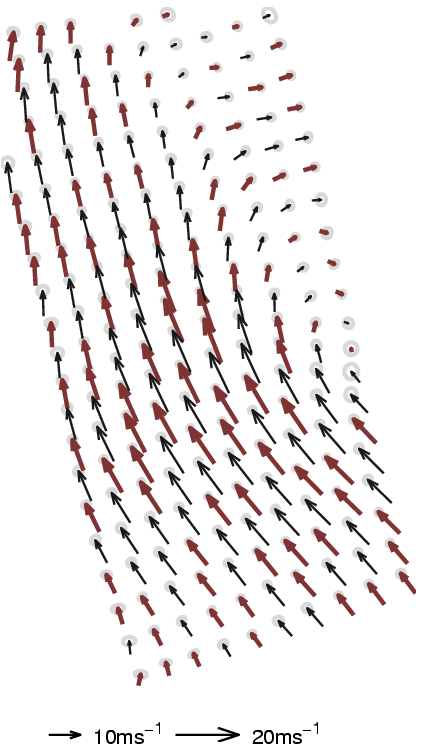
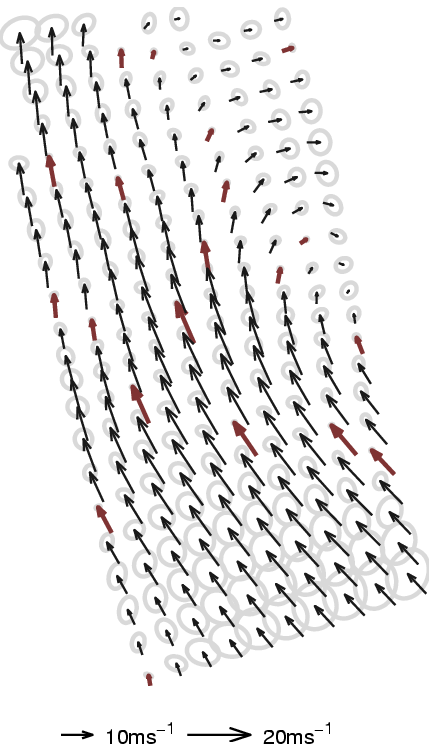
Posterior wind-fields and uncertainties - high number of BVs     Posterior wind-fields and uncertainties - small number of BVs
Figure 2. Results from the same data using the sampling procedure (different colour coding). The left sub-figure shows the inference with a high number of BVs (100) whilst there are only 20 BVs kept to represent the posterior GP. As in the previous case, the uncertainties corresponding to a spatial location is illustrated using ellipses.

Problems

The plots below show the problems one can encounter if using sampling to obtain the update coefficients.
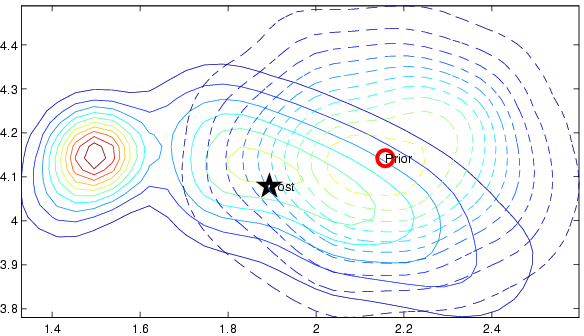
Importance sampling from the posterior     Importance sampling from the posterior - ex. 2
Figure 3. Contour plots of the local Gaussian prior (dashed line) and the posterior computed using importance sampling. We see that the variance along the Y-axis is very elongated, much longer than the associated prior distribution. The iterative approximation trimmed the long tail of the posterior to that of the prior, keeping the inference numerically stable.

Bibliography

The PDF version of this document can be found here.
Questions, comments, suggestions: contact Lehel Csató.