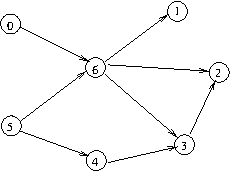
A directed acyclic graph (DAG) is a directed graph having no cycle.
Directed acyclic graphs are often used for representing dependency relations, for example:
DAG example

Cycle-containing graph
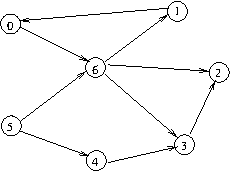
Often, when dependency relations are involved, the following two problems need to be solved:
The latter problem is called topological sorting. Note that the solution is not, generally, unique.
Finding if a directed graph has cycles or not is done while attempting to do the topological sorting.
Property: Topological sorting is possible, for a directed graph, if and only if there are no cycles in the graph.
If a graph has a cycle, then it is obvious that topologically sorting it is impossible: Suppose we have a topological sorting, and let x be the first vertex from the cycle that appears in the topological sorting. Then, let y be the preceeding vertex in that cycle; we have the edge (y,x), but y comes after x in the topological sorting, which is not allowed.
For proving the other way round, we use the construction algorithms below. We'll prove that neither one fails unless there is a cycle in the input graph.
The ideea is the following: we take a vertex with no predecessors, we put it on the sorted list, and we eliminate it from the graph. Then, we take a vertex with no predecessors from the remaining graph and continue the same way.
Finally, we either process all vertices and end up with the topologically sorted list, or we cannot get a vertex with no predecessors, which means we have a cycle. Indeed, if, at some point, we cannot get a vertex with no predecessors, we can prove that the remaining graph at that point has a cycle. Take a vertex, take one of its predecessors (at least one exists), take a predecessor of its, and so on, obtaining an infinite sequence. But the set of vertices is finite, so, we must have repeating vertices, i., e., a cycle.
It remains to get an efficient way to implement finding vertices with no predecessors and removing them from the graph. Here, the idea is to not actually remove vertices, but to keep, for each vertex, a counter of predecessors still in the graph. The algorithm follows:
Input:
G : directed graph
Output:
sorted : a list of vertices in topological sorting order, or null if G has cycles
Algorithm:
sorted = emptyList
Queue q
Dictionary count
for x in X do
count[x] = indeg(x)
if count[x] == 0 then
q.enqueue(x)
endif
endfor
while not q.isEmpty() do
x = q.dequeue()
sorted.append(x)
for y in Nout(x) do
count[y] = count[y] - 1
if count[y] == 0 then
q.enqueue(y)
endif
endfor
endwhile
if sorted.size() < X.size() then
sorted = null
endif
This is based on the Murphy's law whatever you're starting to do, you realize something else should have been done first. Only that, when we discover that, we do that something and, finally, do our activity. This leads to the following simplified algorithm:
do(x):
for y in Nin(x)
if y not yet done then
do(y)
endif
endfor
actually do x
Performing the above requires:
The result is:
Input:
G : directed graph
Output:
sorted : a list of vertices in topological sorting order, or null if G has cycles
Subalgotithm TopoSortDFS(Graph G, Vertex x, List sorted, Set fullyProcessed, Set inProcess)
inProcess.add(x)
for y in Nin(x)
if y in inProcess then
return false
else if y not in fullyProcessed then
ok = TopoSortDFS(G, y, sorted, fullyProcessed, inProcess)
if not ok then
return false
endif
endif
endfor
inProcess.remove(x)
sorted.append(x)
fullyProcessed.add(x)
return true
Algorithm:
sorted = emptyList
fullyProcess = emptySet
inProcess = emptySet
for x in X do
if x not in fullyProcessed then
ok = TopoSortDFS(G, x, sorted, fullyProcessed, inProcess)
if not ok then
sorted = null
return
endif
endif
endfor
Property: A directed graph is a DAG if and only if it has no loops and each of its strongly connected components consists in a single vertex.
Proof: A DAG obviously cannot have loops. In addition, if there are two distinct vertices x and y in the same strongly connected component (SCC), then there is a path from x to y and a path from y to x and those paths together form a cycle; therefore, in a DAG, any SCC can have at most 1 vertex. For the other way round, let's prove that a graph with no loops and with only 1-vertex SCCs is DAG. Suppose the contrary, that we have a cycle. If the cycle has length 1, it is a loop. If the cycle is longer, it has at least 2 vertices, which lie in the same SCC. Thus, we have a contradiction.
Note the similarity between the topological sorting DFS-based algorthm and the algorithm for determining the SCCs. This is not a coincidence and, moreover, the SCC algorithm finds the SCC in a topological order, in the condensed graph defined below.
Given a graph G that may have cycles, we can construct the condensed graph G' as follows: each SCC of G appears as a vertex of G', and we put an edge (A, B) in G' if and only if there is at least an edge in G between a vertex of component A and a vertex of component B.
It is easy to see that G' is a DAG. Moerover, the SCC algorithm determines the SCCs in a topological order with respect to G'.
Input: you are given a list of activities to be done for a project, and each activity has a list of prerequisite activities and a duration
Output: a scheduling of the activities (the starting and the ending time for each activity). If activity B depends on activity A, then B must start when or after A ends; however, two activities that do not depend on each other can be executed in parallel.
The goal is to execute the project as quickly as possible - from the time the first activity or activities start, to the time the last activity or activities end.
There may be several valid scheduling, all yielding the same total project duration. Two of them are more interesting:
Example
| Act. | Prerequisites | Duration | Earliest | Latest |
|---|---|---|---|---|
| 0 | - | 1 | 0-1 | 1-2 |
| 5 | - | 2 | 0-2 | 0-2 |
| 6 | 0,5 | 5 | 2-7 | 2-7 |
| 4 | 5 | 1 | 2-3 | 6-7 |
| 1 | 6 | 2 | 7-9 | 8-10 |
| 3 | 4,6 | 2 | 7-9 | 7-9 |
| 2 | 3,6 | 1 | 9-10 | 9-10 |