Róth Ágoston, a Matematika és Informatika Kar egyik fiatal oktatója és aktív kutatója, 2008 februárjában vált tanársegéddé egyetemünk akkori Numerikus Analízis és Statisztika Tanszékén, jelenleg pedig docensként tanít a Magyar Matematika és Informatika Intézetben. Numerikus analízisre, számítógépi grafikára, számítógéppel segített geometriai modellezésre, Riemann–Finsler-differenciálgeometriai elemekre, differenciálegyenletekre, nemkonvex és nem feltétlenül sima optimalizációs feladatok megoldásait lokalizáló sztochasztikus keresési eljárásokra (például Monte-Carlo-módszerekre és genetikus algoritmusokra) épülő kutatási területe alkalmazott és interdiszciplináris jelleget ölt.

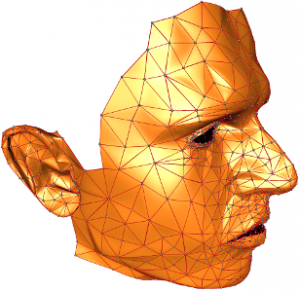
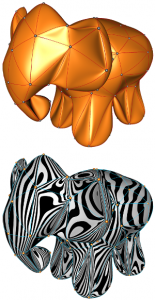A számítógéppel segített geometriai modellezés tudományterület olyan nyílt és zárt, általában sima görbék és felületek leírását, valamint interaktív alakváltoztatását tanulmányozza, amelyeket egyrészt információvektorok (például pozíciót rögzítő kontrollpontok, valamint azokhoz tartozó magasabb rendű deriváltak) halmazával, másrészt pedig (szakaszonként) polinomiális, trigonometrikus, hiperbolikus, algebrai-trigonometrikus, algebrai-hiperbolikus, vagy általában különféle kiterjesztett Csebisev-függvényterek egyértelmű nemnegatív normalizált B-bázisával adunk meg.

Felhasználási lehetőségeinek révén az alkalmazott matematikának ez az ága szorosan kapcsolódik (a) mérnöki alkalmazásokhoz (például építő- és gépiparhoz, elektronikus tervezéshez, gyártási folyamatok automatizálásához, idevágó mérnöki szoftverekhez vagy akár számítógépi játékokhoz), továbbá (b) numerikus analízishez kötődő adatillesztéshez (például adatpontok interpolációjához és approximációjához) is.

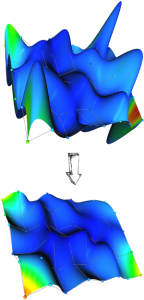Folytonossági és interpolációs feltételek biztosítása mellett sokszor olyan minimális energiaváltozásra (például minimális ívhosszra, minimális hajlítási energiára, minimális felszínre, minimális négyzetes középgörbület-változásra, minimális teljes görbületre, minimális umbilikus eltérésre vagy izoperimetrikus jellegre) vonatkozó megszorításokat is biztosítani kell, amelyeket olyan vonal- vagy felületi integrálokkal (funkcionálokkal) írhatunk le, amelyek egyrészt alulról korlátosak, másrészt pedig – amennyiben lehetséges – paraméterezéssel, egyenletes skálázással, valamint merevtest-mozgásokkal szemben invariánsak. Ilyenkor általában olyan nemkonvex és nem feltétlenül sima optimalizációs feladatokhoz jutunk, amelyek például (a) ismert adatpontokkal, de ismeretlen csomóvektorral leírt interpolációs feltételeket kielégítő görbék és felületek funkcionál-alapú optimalizálásakor, (b) különféle Riemann–Finsler-terek geodetikus vonalainak detektálásakor, utóbbiaktól függő metrikus összefüggések ellenőrzésekor és egyéb költségfüggvények kritikus pontjainak beazonosításakor jelennek meg.

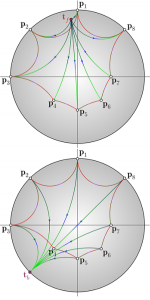A Riemann–Finsler-geometria a görbült metrikus terekre jellemző jelenségeket (például geodetikus vonalak, minimálfelületek, vagy egyéb görbülettől függő fogalmak létezését) tanulmányozza. A klasszikus euklideszi geometriával szemben, az iránygörbülettől függő tér belső szerkezetét figyelembe véve, a Riemann–Finsler-geometria sokkal pontosabban írja le a geometriai fogalmakat, továbbá mély elméleti vonatkozásai mellett olyan gyakorlati felhasználhatósági lehetőségekkel is rendelkezik, amelyek például (a) valamely valószínűségi sűrűségnek a görbült tér egyik pontjából egy másikba történő optimális átvitelt biztosító pályagörbék leírásakor; (b) nemeuklideszi környezetben mozgó entitások (például űrhajók, vagy idegimpulzusok) pályagörbéinek meghatározásakor; vagy (c) geodetikus terekben egyensúlypontok leírásakor és modellezésekor (például közgazdaságban fontos, általánosított Nash- és Stackelberg-típusú pontoktól függő optimalizációs feladatokban) jelennek meg.

A bemutatott, informatív jellegű képek Róth Ágoston szakcikkeiből származnak, amelyeket a Thomson Reuters/Web of Science adatbázis által jegyzett, nemzetközileg elismert Computer Aided Geometric Design, Computer-Aided Design, Journal of Optimization Theory and Applications és a Journal of Computational and Applied Mathematics szakfolyóiratokban közölt.

2011. október 5. és 2014. szeptember 30. között a CNCS-UEFISCDI által támogatott Emberi Erőforrások program keretén belül a Recent problems in Computer Aided Geometric Design című, PN-II-RU-TE-2011-3-0047 kódú nemzeti projekt igazgatója volt. 2013. szeptember 1. és 2014. december 31. között az Európai Szociális Alap és Magyarország által támogatott, fiatal oktatóknak és kutatóknak meghirdetett, TÁMOP-4.2.4.A/2-11/1-2012−0001 azonosítójú Neumann János Nemzetközi Ösztöndíjban részesült. 2015. november 14-én a Magyar Tudományos Akadémia Kolozsvári Akadémiai Bizottsága Fiatal Kutatói Díjjal tüntette ki a természettudományok területén elért eredményeiért.

Oktatói tevékenységei számítógépi grafikához, geometriai modellezéshez, valószínűség-számításhoz és matematikai statisztikához kötődnek. Kutatási területére képes hallgatókat is vonzani, amit az általa vezetett diákok hazai, vagy külföldi tudományos diákkonferenciákon elért díjai is alátámasztanak. Akárcsak az előző években, az elkövetkezőkben is számítunk az egyetemünk által szervezett diákkörökben és hallgatói táborokban zajló rendszeres előadásaira.

Források:
A Babeş–Bolyai Tudományegyetem honlapja
A BBTE Magyar Matematika és Informatika Intézet oktatói
Róth Ágoston kutatói oldala